ベルヌーイの定理
ベルヌーイの定理とは、流体の単位質量あたりのエネルギーを示す式で、圧力に加えて、内部エネルギー、運動エネルギー、位置エネルギーの4種類のエネルギーの総和は常に一定であることを示している。1738年、ダニエル・ベルヌーイによって発見された。
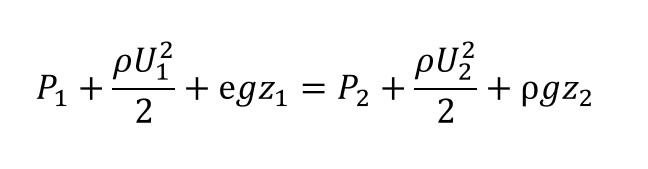
ベルヌーイの定理
ベルヌーイの定理は、流路内の地点1(面積A1、流速U1、密度ρ、高さz1)から、地点2(面積 A2、 流速 U2,密度ρ、高さz2)への非粘性流体の流れを想定したとき、次の式のようになるが、これをベルヌーイの定理という。この式からわかる通り、地点1と地点2のエネルギーの総和は同じになり、地点2が地点1に比べて、圧力(P)と位置エネルギー(ρgz)が大きくなれば、運動エネルギーは(ρU2/2)は低くなることがわかる。また高さが同じ場合、地点1と地点2位置エネルギーは同じになるので、圧力(P)+運動エネルギー(ρU2/2)のみに着目して、地点1・地点2を考えればよい。
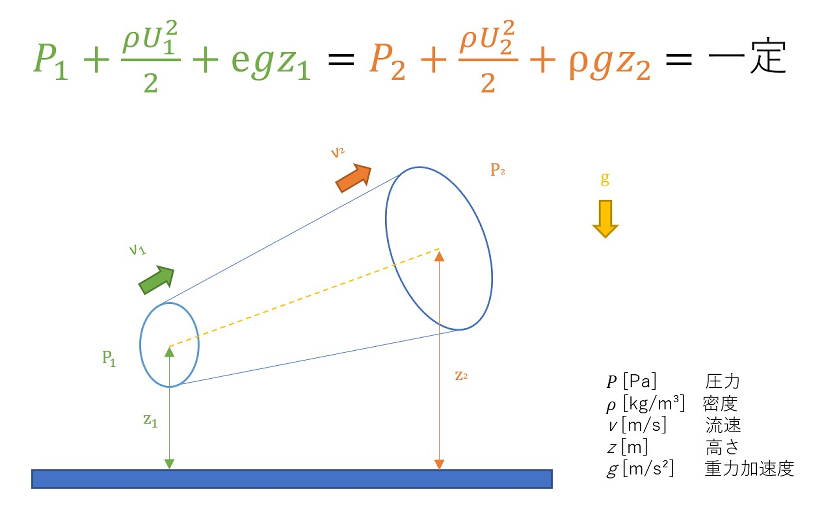
上述した通り、ベルヌーイの定理は圧力、運動エネルギー、位置エネルギーの合計でわかる。なお、ベルヌーイの定理では理想流体を想定し、密度は一定で非粘性(摩擦力などの影響を考えない)なので内部エネルギーは一定であるため、その影響は無視する。
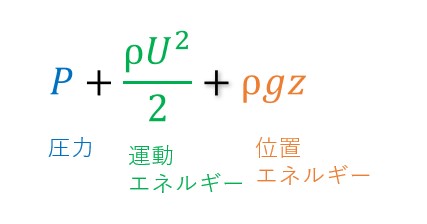
全圧(静圧+動圧)
Pを静圧、ρU2/2を動圧といい、その合計したP+ρU2/2を全圧という。高さが同じで無視できる場合、全圧を考慮するとよい。

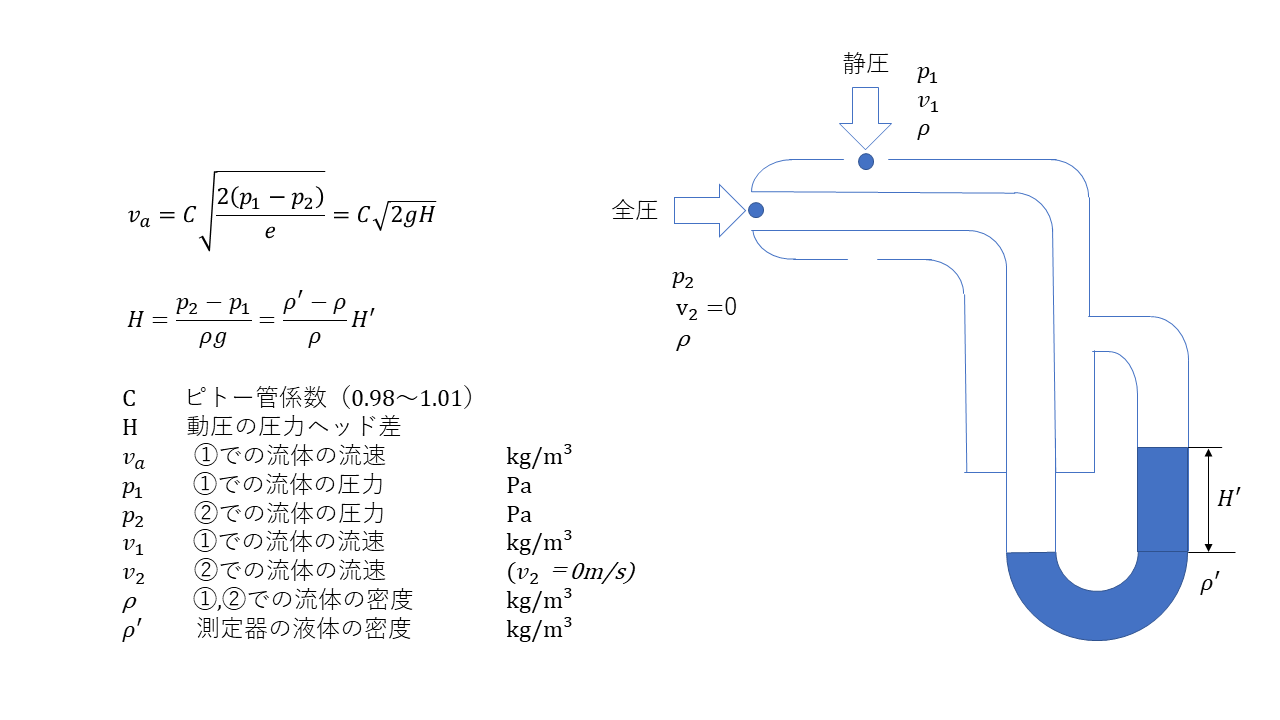
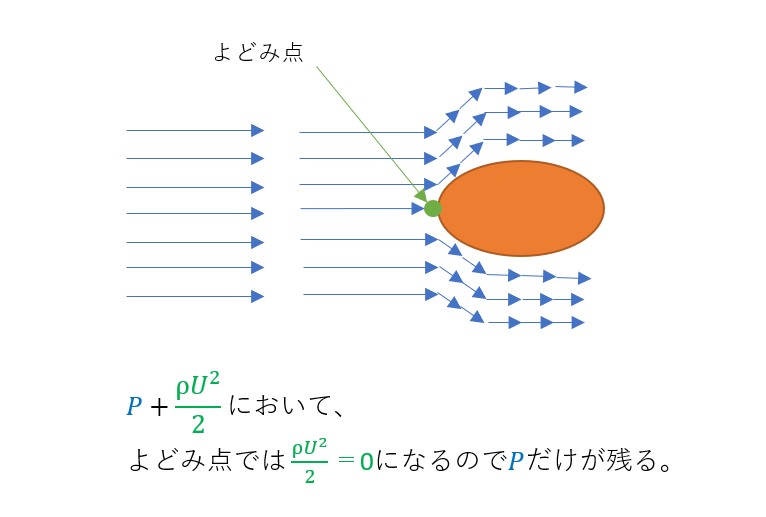
よどみ点
流体の中で、速度が0になる点をよどみ点という。また、そのときの圧力をよどみ圧という。
ベルヌーイの定理の応用した測定器具
ベルヌーイの定理を応用した測定として、ピトー管、オリフィス流量計、ベンチュリー流量計がある