カルノーサイクル Carnot cycle
カルノーサイクルとは、フランスのカルノー(Nicolas Leonard Sadi Carnot)によって考案された、高温熱源から熱エネルギーを得て、その一部から仕事を行い、残りの熱を低温熱源に戻す、という熱機関のサイクルである。ただし、等温変化で受熱と排熱をするため、カルノーサイクルで作動する内燃機関は存在しなせず、理論最大熱効率を考察するための理想モデルである。
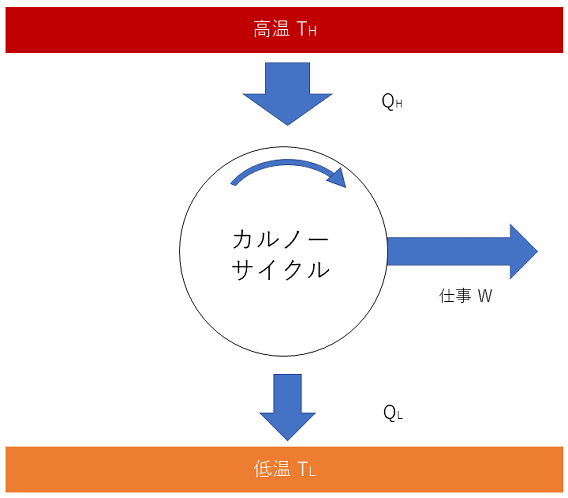
カルノーサイクルのモデル
カルノーサイクルのモデルとは、温度THの高温熱源から熱量QHを取り入れて、その一部を外部への仕事Wに変換してから、残りの熱量QLを温度TLの低温熱源へ捨てる、という動作を繰り返していくサイクルである。
P-V線図
P-V線図とは、物体の圧力Pと体積Vとを直交座標の両軸にとって状態変化を表した線図である。カルノーサイクルは2つの等温変化(等温膨張、等温圧縮)と2つの断熱変化(断熱圧縮、断熱膨張)の変化からなるもので、準静的過程と仮定した可逆サイクルである。
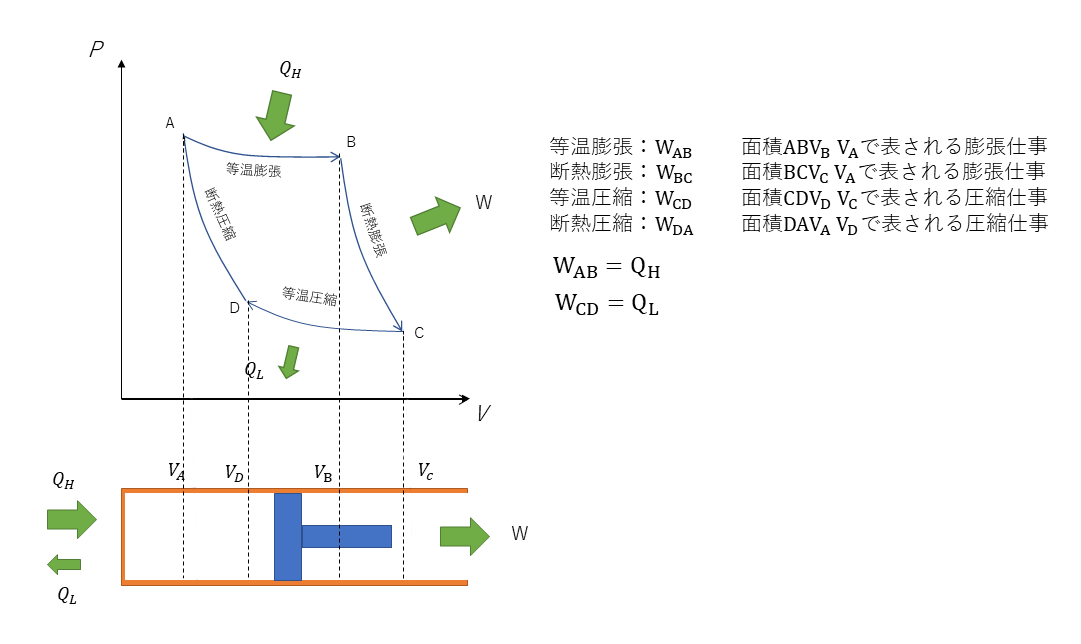
A→Bの過程:等温膨張
A→Bの過程とは、等温膨張の過程である。高温における等温給熱過程であり、シリンダ内の気体は、外部からの熱を吸収することによって、状態AからBに膨張していく。内部の温度は、温度THの高温熱源から熱量QHを取り入れて状態AからBに変化するので、準静的過程であるためには、高温熱源THと同じ温度で変わらず等温膨張となる。
B→Cの過程:断熱膨張
B→Cの過程とは、断熱膨張の過程である。 高温熱源からの熱量QHが遮断されて、状態BからCに膨張します。熱の出入りがなく膨張するために温度が下がり、低温熱源のTLに等しくなるまで膨張する。断熱変化で外に対して仕事Wをしているために、内部エネルギーは減少して温度はTHからTLに下がる。この過程は、断熱冷却の過程で断熱膨張となる。
C→Dの過程:等温圧縮
C→Dの過程とは、等温圧縮の過程である。内部の気体が低温熱源のTLと同じ温度になり、低温熱源に触れた状態で体積を減少させる過程となる。外部から仕事を得て、状態CからDに圧縮される間に熱が出るが、その熱量QLは温度TLの低温熱源へ捨てられる。この過程は、元の状態に戻すために必要な部分で、低温における等温放熱の過程で等温圧縮となる。
D→Aの過程:断熱圧縮
D→Aの過程とは、断熱圧縮の過程である。低温熱源から切り離されて、状態Dから最初のAに圧縮されて戻る。外部からの仕事を得て圧縮されるが、その間に熱が外に出ないため、内部の気体は高温熱源の温度THまで上昇する。この過程で元の状態に戻るが、断熱における昇温の過程で断熱圧縮となる。
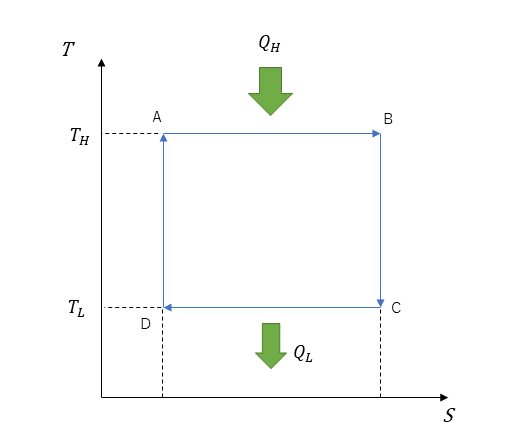
T-S線図
サイクル仕事
サイクル仕事は次式の通りになる。

カルノーサイクルの受熱量と排熱量の比
カルノーサイクルの受熱量と排熱量の比はQH/QL=TH/TLと表される。

カルノーサイクルのサイクル効率
カルノーサイクルのサイクル効率は下記の次式で表される。ここにおける熱効率とは、カルノーサイクルが高温熱源から受け取った熱量のうちの仕事に変換できた量を示す指標となる。 供給された熱量QHのうちで、外部に対して成す正味の仕事をWとして低温熱源へ捨てられる熱量をQLと考える。 A→B→C→D→Aのサイクルのなかで、この間に外部に行った仕事はW=QH-QLとなる。 なお、外燃機関であるスターリングエンジンの理論効率はカルノーサイクルと同じになる。(参考:スターリングサイクル)

カルノーサイクルの計算例1
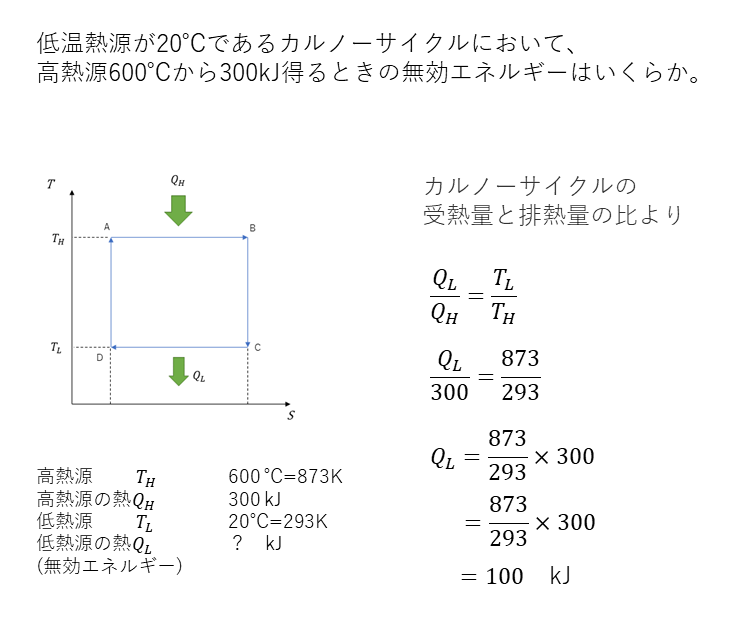
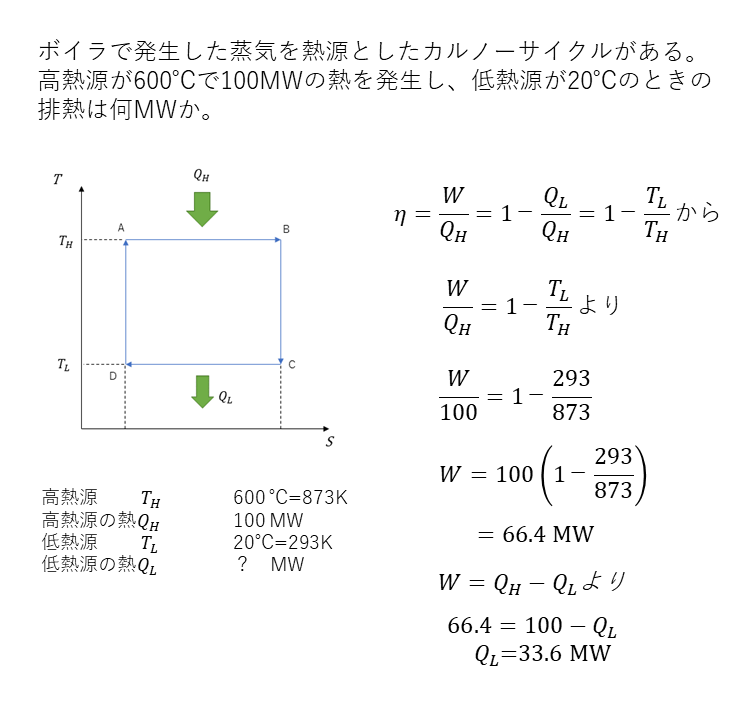
カルノーサイクルの計算例2
逆カルノーサイクル
逆カルノーサイクルとはカルノーサイクルの仕組みを逆にしたサイクルである。冷凍機やヒートポンプとして利用される。