エントロピー entropy
エントロピーとは、en と「変化」を意味するギリシア語の tropy を合わせた言葉で、分子の乱雑さを示している。熱力学では、加えられる熱量に対して、そのときの温度Tで割ったものと定義される。単位[J/K]。ドイツの理論物理学者であるクラウジウスが熱力学で導入した概念だったが、現在では、哲学、生物学、環境学、情報科学など広く使われる概念となり、広義の意味を持つようになった。
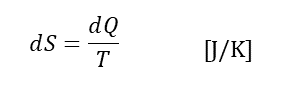
エントロピーのイメージ

熱力学とエントロピー
熱力学第二法則に基づき、カップに入ったコーヒーがいずれ冷めるように、熱は熱いものから冷たいものへ移動するが、その逆は生じない。このような不可逆現象においてはエントロピーは増大し、可逆現象では一定となる。(参考 カルノーサイクルのエントロピー)
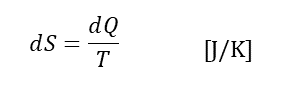
比エントロピー
比エントロピーとは、質量mの物質の単位質量あたりのエントロピーである。

エントロピー増加の法則
自然界では、エントロピーが常に増加していくことになる。このような法則をエントロピー増加の法則という。
生物学とエントロピー
宇宙は拡大し続け、時間の経過とともにエントロピーを増大させ続けている。しかし生物だけは、エントロピーに反し恒常性を維持しようと努めている。ここに生物の特色が認められる。
統計力学とエントロピー
統計力学では、エントロピーをS=kInWと定義し、ボルツマンの公式として知られている。kはボルツマン定数、Wはミクロで見た状態の数である。この式からとることのできる状態の数が増えて分散するとエントロピーが増大することがわかる。ここからstrong>エントロピーはミクロな状態の乱雑さの度合いを表していることがわかる。