ゴルドン・ランキンの式
ゴルドン・ランキンの式とは、座屈に関する式である。ランキンの式とも呼ばれる。オイラーの式が柱の座屈を示しているが、ゴルドン・ランキンの式は破壊(ランキン)によるため、この名が付けれた。
細長比
細長比とは、柱の長さLと断面二次半径kとの比で表される。ゴルドン・ランキンの式が適用するときは、材質による適用範囲に基づかなければならない。

適用範囲
| 材質 | 鋳鉄 | 軟鋼 | 硬鋼 | 木材 |
|---|---|---|---|---|
| L/K | 80以下 | 90以下 | 85以下 | 60以下 |
圧縮破壊応力と定数a
ゴルドン・ランキンの式において圧縮破壊応力と定数aは材料固有の定数として決まっている。
| 材質 | 圧縮破壊応力 Mpa | 定数a |
|---|---|---|
| 鋳鉄 | 330 | 1/7500 |
| 軟鋼 | 480 | 1/500 |
| 硬鋼 | 550 | 1/1600 |
| 木材 | 50 | 1/750 |
拘束係数
柱の拘束の条件によって座屈の起こりやすさやが異なるため、拘束係数Cとして、それぞれ下記の通りで表される。
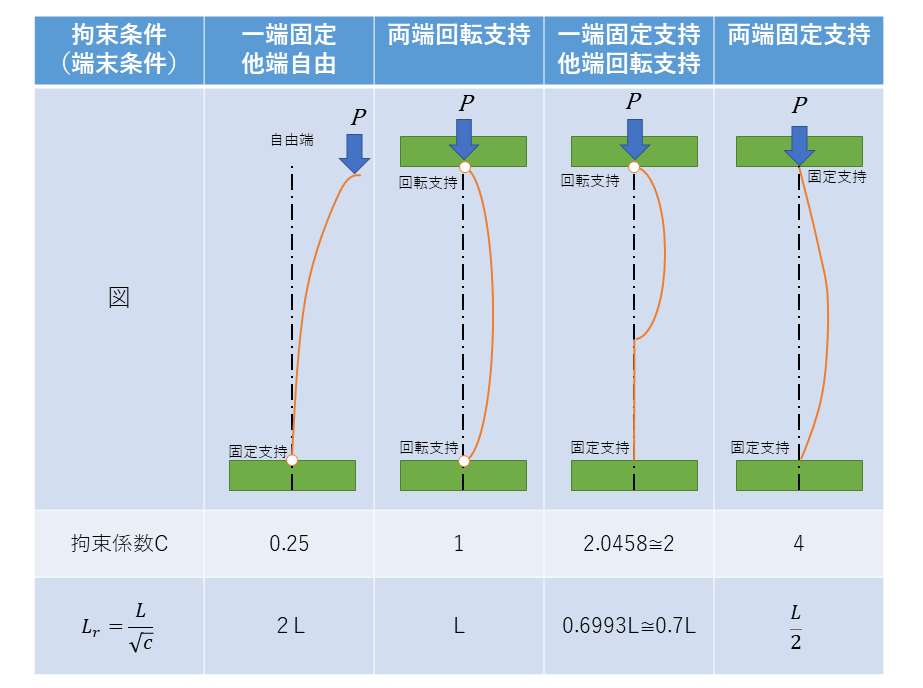
座屈荷重

座屈応力
