オットーサイクル Otto cycle
オットーサイクルとは、ドイツのオットーにより創案されたガソリンエンジンなど火花点火式内燃機関の基本サイクルで、上死点で等容的に受熱することが特徴である。作動流体の加熱および放熱が同じ容積のもとで行われることから等容サイクルとも呼ばれる。断熱圧縮→等容加熱→断熱膨張→等容冷却のサイクルで変化が行われる。
ガソリンエンジン
ガソリンエンジンでは、燃料と空気の混合気を圧縮して、上死点で火花点火し、一気に燃焼させる。そのため、オットーサイクルでは、上死点で瞬間的に受熱すると近似する。
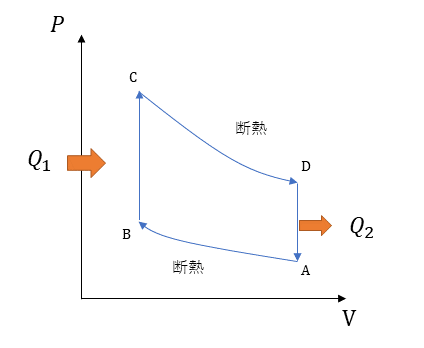
P‐V線図
P-V線図は圧力と体積の関係を示している。
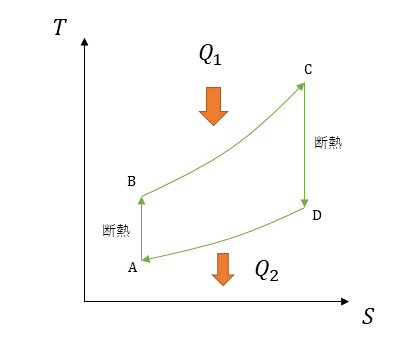
T-S線図
オットーサイクルのサイクル
オットーサイクルは断熱圧縮→等容加熱→断熱膨張→等容冷却のサイクルで行われる。

- 断熱圧縮(状態Aから状態B):面積ABV1V2で表される圧縮仕事WABV1V2
- 等容加熱(状態Bから状態C):燃焼による受熱Q1
- 断熱膨張(状態Cから状態D):面積CDV1V2で表される膨張仕事WCDV1V2
- 等容冷却(状態Dから状態A):排気による放熱Q2
A→B 断熱圧縮
A→Bの断熱圧縮では、断熱状態(等エントロピー状態)で内部の混合ガスを圧縮することで温度があがる。
B→C 等容加熱
B→Cの等容加熱は、断熱圧縮された混合ガスが、Bで点火プラグで着火して熱が与えられるが、容積が一定のため圧力が上昇する。(V=一定,dV=0)
C→D 断熱膨張
C→Dの断熱膨張では、断熱膨張しながらピストンを押し下げて外部に仕事をする。
D→A 等容放熱
D→Aの等容放熱では、等容(V=一定,dV=0)でシリンダ内に残っている熱を排出することで圧力が下がるため、元の状態に戻る。
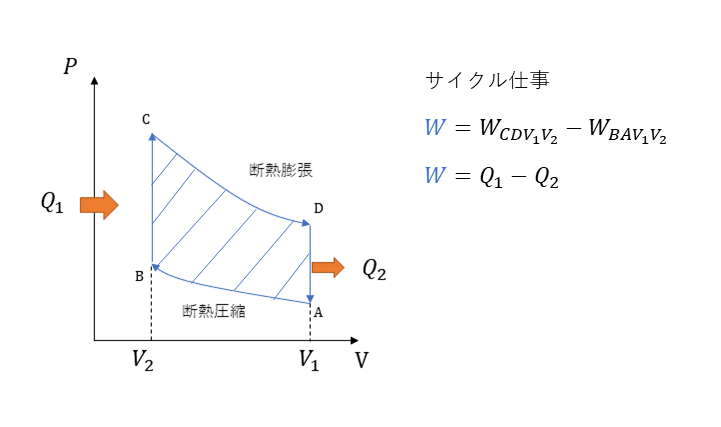
サイクル仕事 W
サイクル仕事は下記の通り、膨張仕事から圧縮仕事を引くことで求められる。熱力学の第一法則より熱量Q1からQ2を引くことで求められる。このとき、エネルギーを100%仕事に利用されることなく、損失が存在することがわかる。
熱効率
熱効率は下記の式で表される。燃焼によって発生した熱Q1のすべてを仕事Wに変換することはできなく排気エネルギーとして使われる。これはオットーサイクルが熱力学第二法則に基づくことを示している。
オットーサイクルの理論効率
オットーサイクルの理論効率は次式で表される。 比熱比は作動流体に依存するため圧縮比が大きくなるほど効率も高くなることがわかるため、エンジン開発では、圧縮比を高めることが一つの重要ポイントとなる。

理論効率のグラフ
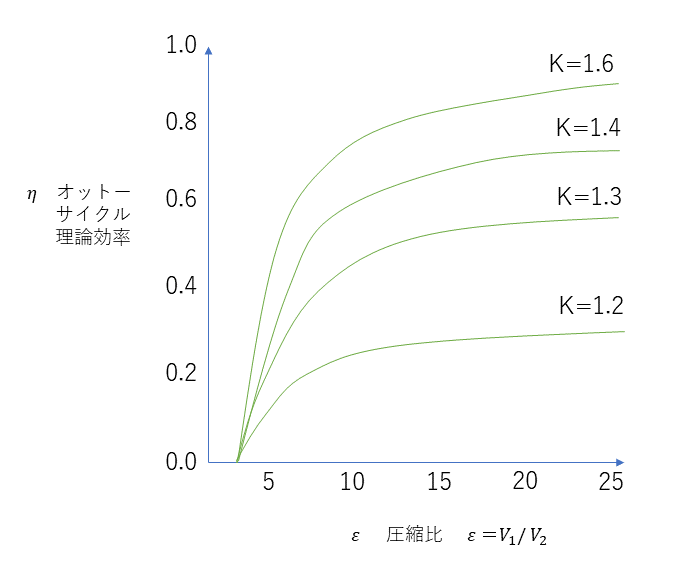
圧縮率を向上させたときのの理論効率
