単振動
単振動は単純な振動で、単振動は常に振動の中心に向かう復元力が働き続けることによって継続する。機械や内燃機関の振動は単振動の組み合わせでできている。単振動は騒音の原因となるため、防振ゴムなどを入れる。運動の第二法則が基本原理である。
正弦関数
単振動は、正弦関数で表すことができる。下記の変位、速度、加速度に表されるように等速円運動の正射影と見なすことができる。このとき、点Pは半径r[m]の 円周上を速さv0[m/s]で等速円運動をしている。正投影を表す点Pは点Pが円周上を一周する間に、点Oを中心とする距離2rの区間を一往復する。

変位、速度、加速度
点Pが点Aから反時計回りに等速回転運動を始めると、その正投影である点Pは点Oから右向きに動き出す。ここで ω [rad/s] は角速度であり、θ = ωtの関係がある。
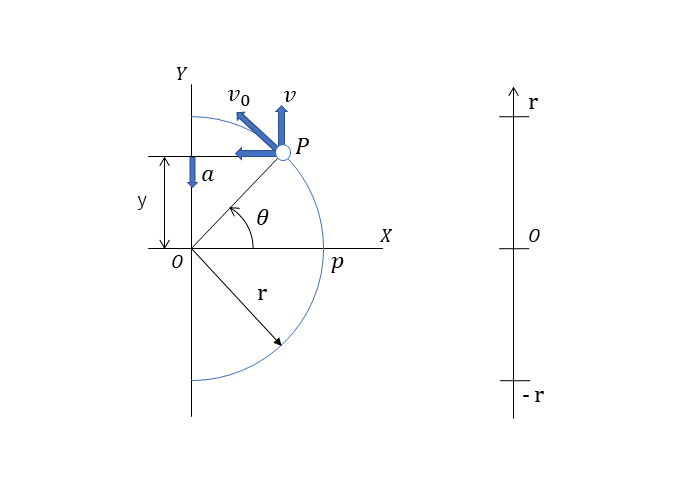
変位
x= rsin0 = r sin ωt [m] ここで、変位x[m]の最大値であるr [m] を振幅、また θ[rad] を 位相という。
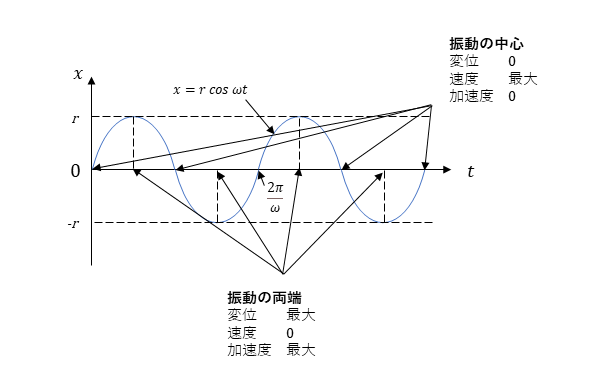
速度
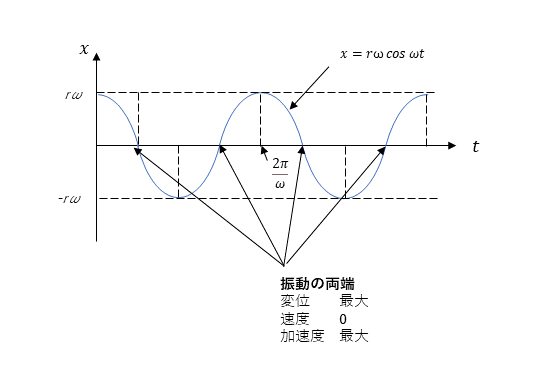
速度の式
速度v[m/s]の式は、変位x[m]を微分することで求めることができる。
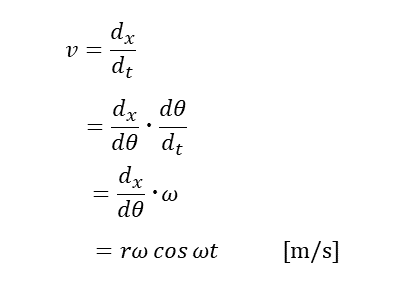
加速度のグラフ
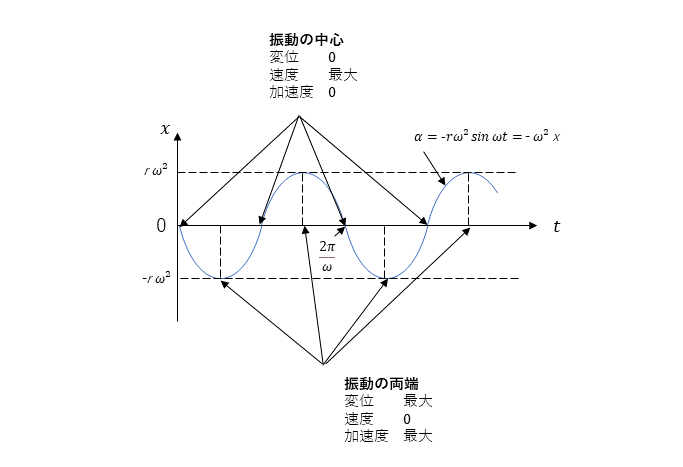
加速度の式
加速度は、速度v[m/s] を微分することで求めることができる。
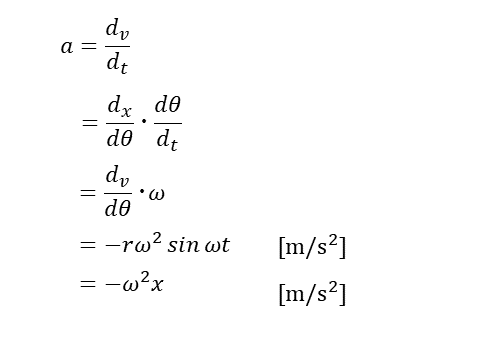
周期
周期とは単振動が一往復する時間をいい、振動数とは、周期の逆数で1秒間の往復回数をいう。単位は1ヘルツ(Hz)。

固有振動数と周期・振動数の関係
周期と振動数は次式によって求められるが、これは単振動の運動方程式から角速度を代入することで求めることができる。
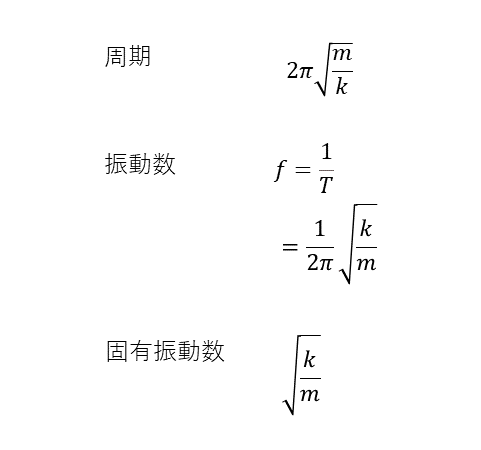
単振動に働く力(復元力)
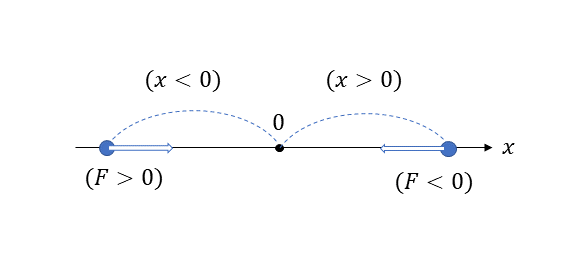
単振動をする物体に働く力は、単振動の加速度を表す式を運動方程式に代入することで導くことができる。次式からFがマイナス方向つまり、復元する方向に力が働くことがわかる。この力を復元力といい、特に力の大きさが変位の距離に比例する場合を線形復元力という。
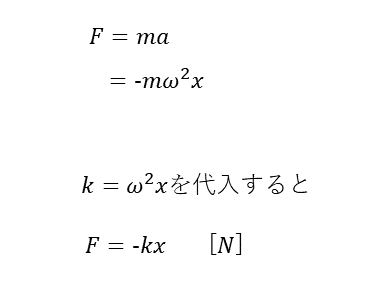
線形復元力
固有振動数
単振動に関する下記の式を固有振動数という。固有振動数は周期や振動数に重要な式である。
