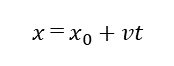速度
速度とは、物体が動くときの速さと同じような意味で、距離/時間で定義される。特に同じ速度で動くものを等速直線運動といい、速度×時間で距離を示される。また、実際の運動は瞬間、瞬間で速度が異なる。その平均をとる速度を平均速度、瞬間瞬間で動くものを瞬間速度という。また、実際の運動には加速度が加わったり、摩擦や空気抵抗によって速度が遅くなることも考慮が必要である。
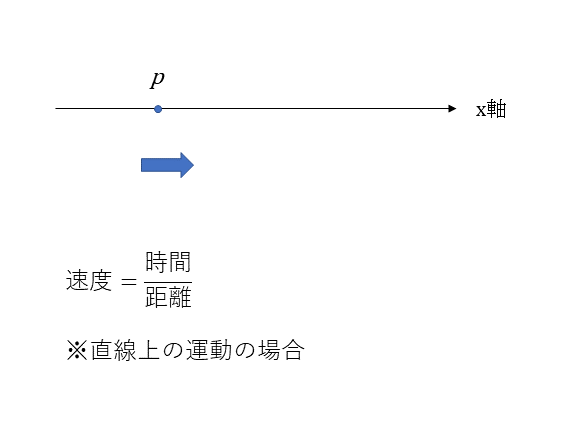
直線運動
直線運動とは、一直線上の運動である。MKS単位系を使い、長さをm、時間をsで表す。下記の図の通り、x軸上に 座標原点Oを選び、時刻tにおける位置Pの座標をxとすると、xが決まると運動が決まってくる。一般に、物体の運動を表す変数の数を運動の自由度といい、直線運動では運動の自由度は1である。
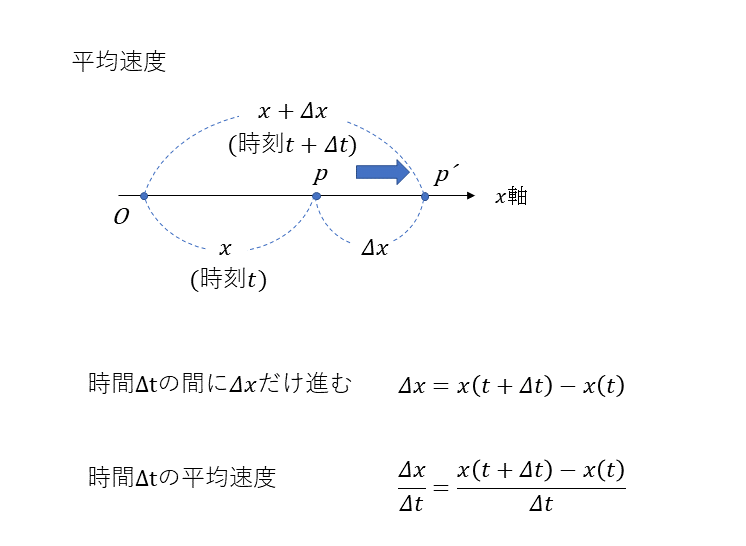
平均速度
平均速度とは、時刻tから微小時間Δt後の時刻t+Δt における位置P’の座標をx + Δx とする。時間Δtの間に電車はΔx だけ進むとする。あるいは、xはtの関数であるが、これをx(t) と書けば、下記で表され、Δtの間の速さを平均速度がわかる。
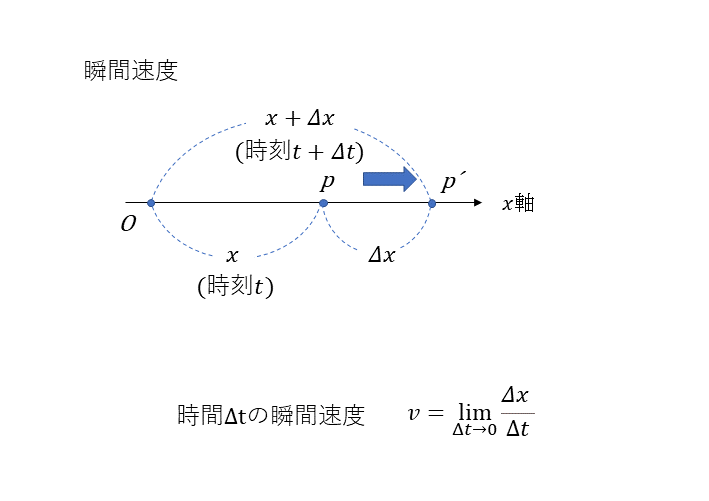
瞬間速度
Δt→0の極限をとるとことで、一定の値vに近づくが、vを時刻tにおける速度を瞬間速度という。(速さとは物理的には瞬間速度のことをいう。)長さを時間で割った次元をもち、その単位はm・s−1である。
瞬間的な速度の幾何学的意味
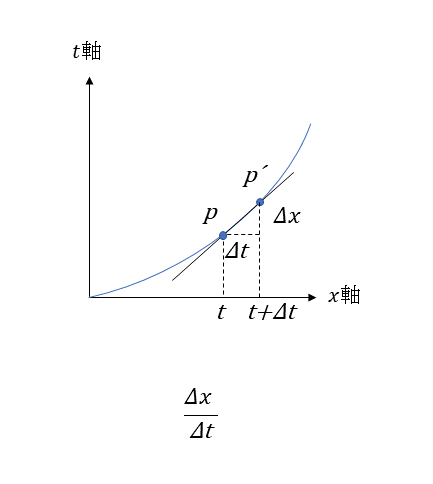
座標を時間tの関数として図示したとき、xは下記のような曲線で表されるとすると、tとt + Δt との間における平均速さΔx/Δtは図の直線PP’の傾きに等しい。Δtを0に近づけると、点P’は点Pに接近し、直線 PP’はこの極限で点Pにおける曲線への接線と一致する。すなわち、瞬間の速さは点Pでの接線の傾きに等しい。
等速直線運動
等速直線運動とは、速度が一定であるような直線運動を等速直線運動という。時間が0、すなわちt=0における物体の座標をx0とする。(このように最初の時間における条件のことを初期条件という)速度は一定であるから、時間がtだけたつと物体は右の方にvtだけ進む。