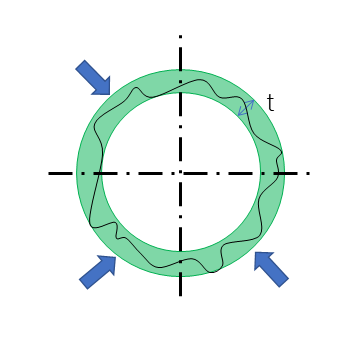
真円度
真円度(Roundnes)とは、円の丸さを示す幾何公差である。JISでは、円形形体の幾何学的に正しい円からの狂いの大きさ、と定義されている。形状公差のひとつで基準を示すデータムは必要ない。
真円度1
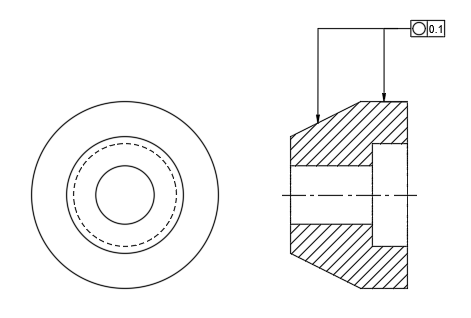
真円度について、円筒(または円錐形状)に真円度を指示する場合が下記であるが、この図では、「軸に直角な任意の断面において、半径距離で0.1だけ離れた二つの同心の円の間に規制される」ことを意味している。
真円度2
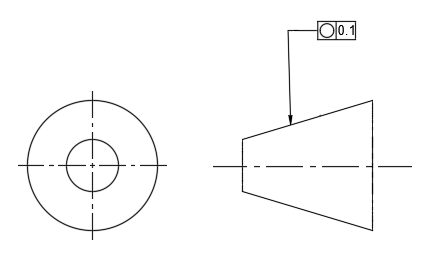
次に下の図では、円筒部とテーパ部両方に真円度0.1を指示している。これは、「円筒部・テーパ部ともに、軸に直角な任意の断面において、半径距離で0.1だけ離れた二つの同心の円の間に規制される」ことを意味している。
真円度の公差域の求め方
真円度の公差域は測定した際に、半径方向で公差値分だけ離れた二つの円の間になければならない。決め方には、一般的に最小二乗平均法、最小領域法、面積重心法、内接円法、外接円法がある。
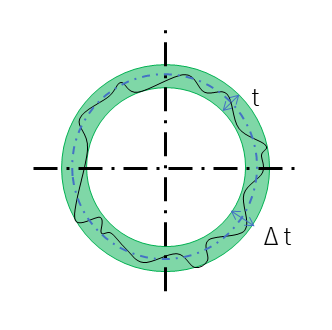
最小二乗平均法
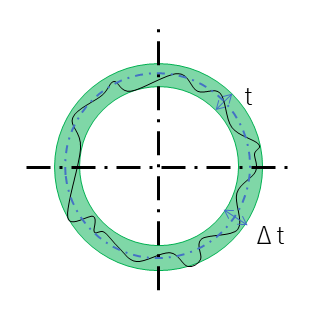
最小二乗平均法とは、理想とする中心円を描き、その円から実際に測定した円の値がどれほど離れたかを見る方法である。この測定結果が中心円に対し、Δtの標準偏差を求めることで、真円度内にあるかどうかを評価する。
最小領域法
最小領域法とは、実際に測定した円に対して、同心の二つの円で挟んだときに、その円の間隔が最小となる中心を真円度とする方法である。
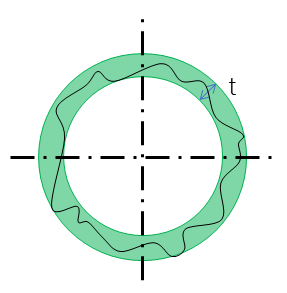
面積重心法
最小二乗平均法のように理想の中心の円を想定し、その距離Δtについて、その総和からその値が最小になるよう計算する方法である。
内接円法
内接円法とは、実際に測定した穴のデータに対し、内側から円状に広げていき、3点で接するところが内接円となり、その中心をこの穴の中心として真円を想定する方法である。
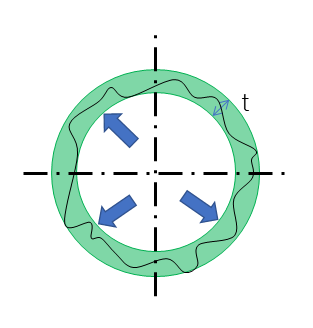
外接円法
外接円法とは、内接円法と同じように実際に測定した軸のデータに対して、外側から円状に挟めていき、3点で接するところが外接円となり、その中心をこの軸の中心として真円と想定する方法である。