理想気体 ideal gas
理想気体(完全ガス)とは実在気体の性質を理想化したもので、実際には存在しない理論モデルである。衝突以外の相互作用がなく、自由に運動する質点として考える気体である。空気、水素、ヘリウム、メタンガスなどは理想気体に近い性質をもつ。
理想気体に近い気体
気体が占めている空間に対して原子・分子が占める空間が小さければ小さいほど、理想気体に近い条件になる。温度が高く気圧が低いほど、理想気体に近い状態になる。
ボイル・シャルルの法則
理想気体では、ボイル・シャルルの法則が成立する。
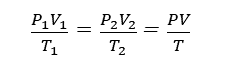
理想気体の状態方程式
理想気体の状態方程式とは、ボイル・シャルルの法則とゲイ・リュサックの方程式に基づく関係式で、圧力と体積の積が気体定数、質量、温度の積と等しくなる。空気、水素、ヘリウムメタン等は下記の式に近い性質をもつ。

気体の質量m
気体の質量mは分子量Mとモル数nの積に等しいので次数のように展開する。

一般気体定数
Roとは、一般気体定数(普遍気体定数)で、すべての理想気体について等しい値になる。 単位は [J/(kg・K)] となる。
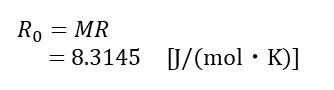
アボガドロ数
アボガドロ数とは、この1molあたりの分子数である。この分子数Nを表すと次式のようになる。

ボルツマン定数
ボルツマン定数とは、一般気体定数をアボガドロ数で割ったもので、分子1個当たりの気体定数である。単位はJ/Kである。(エネルギーの単位であるジュール(J)とケルビン(K)を結びつける定数である。)ミクロな分子でみると、kTという形で重要な定数として出てくる。

ガス定数、標準密度、比熱
下記は理想気体のガス定数、標準密度(101.325kPa,273.15K)、比熱および比熱比(0Pa,273.15K)の目安である。
| 気体 | ガス定数 | 標準密度 | 定圧比熱 | 定容比熱 | 比熱比 |
|---|---|---|---|---|---|
| R | ρ₀ | Cp | Cv | γ | |
| J/(kg・K) | kg/m3 | kJ/(kg・K) | kJ/(kg・K) | – | |
| 水素 | 4124.49 | 0.0899385 | 14.25 | 10.12 | 1.408 |
| 酸素 | 259.837 | 1.42763 | 0.914 | 0.654 | 1.398 |
| 空気 | 287.03 | 1.29236 | 1.005 | 0.718 | 1.400 |
| 二酸化炭素 | 188.924 | 1.963483 | 0.819 | 0.630 | 1.30 |
| 水蒸気 | 461.523 | – | – | – | – |
| アセチレン | 319.33 | 1.16165 | 1.513 | 1.216 | 1.244 |
| メタン | 518.279 | 0.7157 | 2.16 | 1.63 | 1.32 |
理想気体の状態変化
理想気体は体積が一定である定容変化、圧力が一定である低圧変化、温度が一定である等温変化、熱の出入りが行われない断熱変化が行われる。下記のピストンが例にあたるが、理想気体では、摩擦などの熱損失がない可逆変化が想定される。現実では、仕事に変化することはなく不可逆変化しか起こらない。
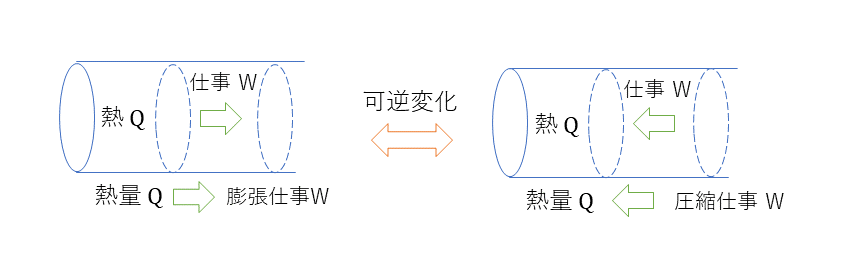
定容変化
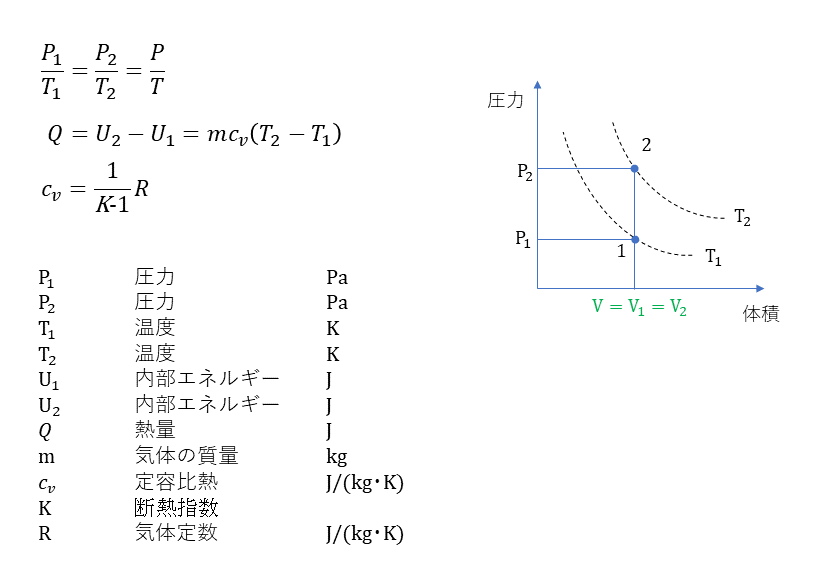
定圧変化
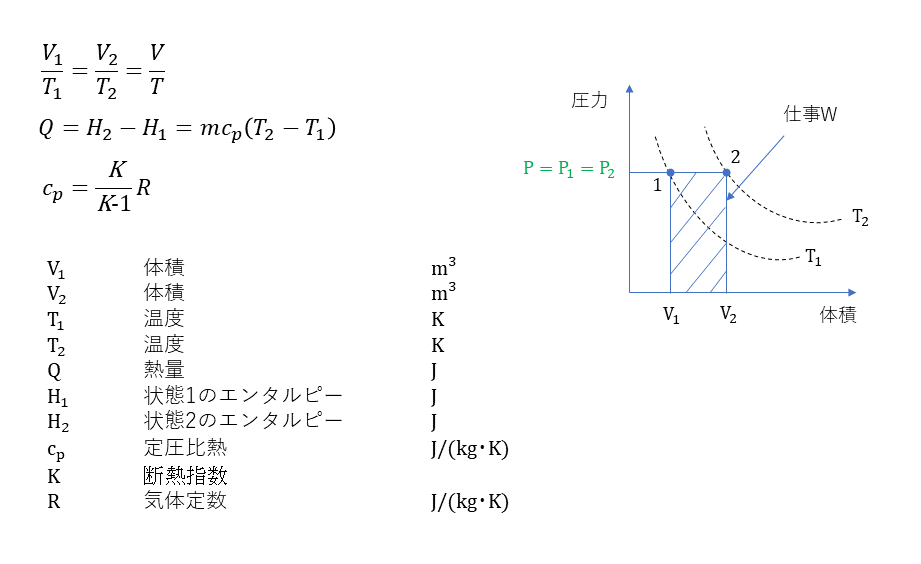
定温変化
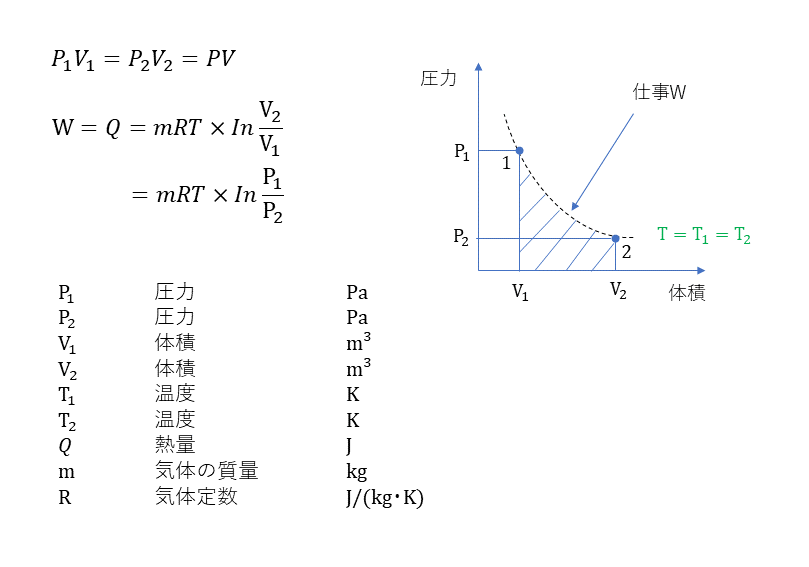
断熱変化
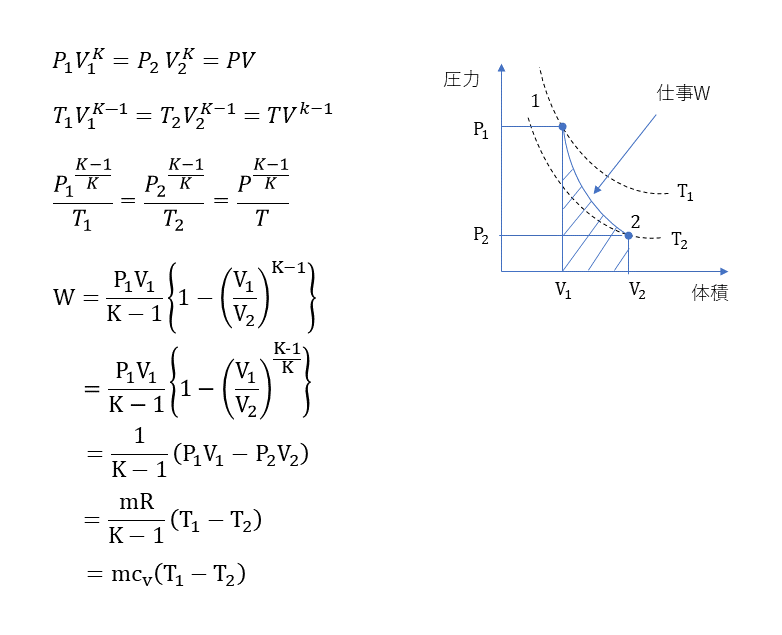
断熱熱落差

準静的過程
準静的過程とは、変化の途中、系も外界も常に熱平衡状態を保つような過程である。しばしば理想気体では準静的過程を想定して考察する。また、準静的過程は可逆過程(現実は不可逆変化)が想定されているため、変化の過程と時間的に逆の過程も成立されるとする。