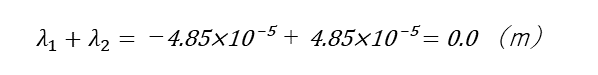材料に加わる引張と圧縮、伸びの計算
下図のような段付き棒(青、緑)に荷重がかかっているケースを考える。ここから部材内部に生じる軸力と引張応力・圧縮応力を導き出す。
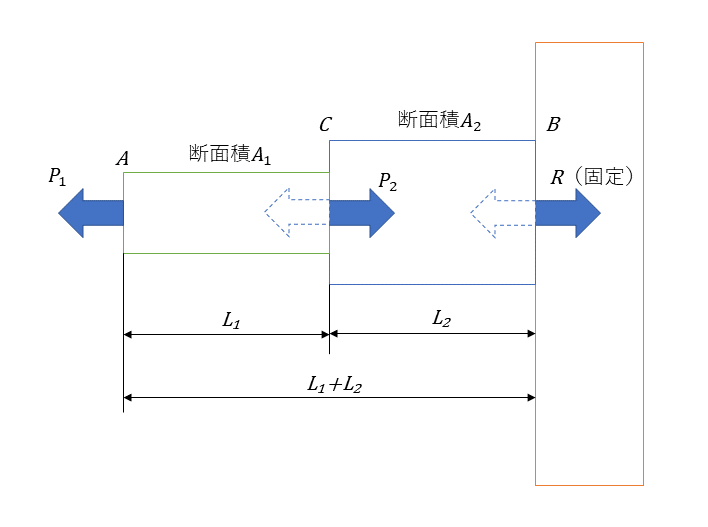
フックの法則とひずみから伸びの公式を求める。
フックの法則とひずみから、伸びがPL/AEが導かれることがわかる。

伸びの公式を使ってそれぞれの伸びを求め合計する。
それぞれの伸びの公式の値が正なら伸びを、負ならば縮みである。

応力
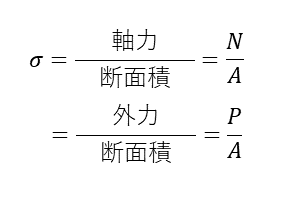
具体的な計算
上記を参考に下記の場合を計算する。
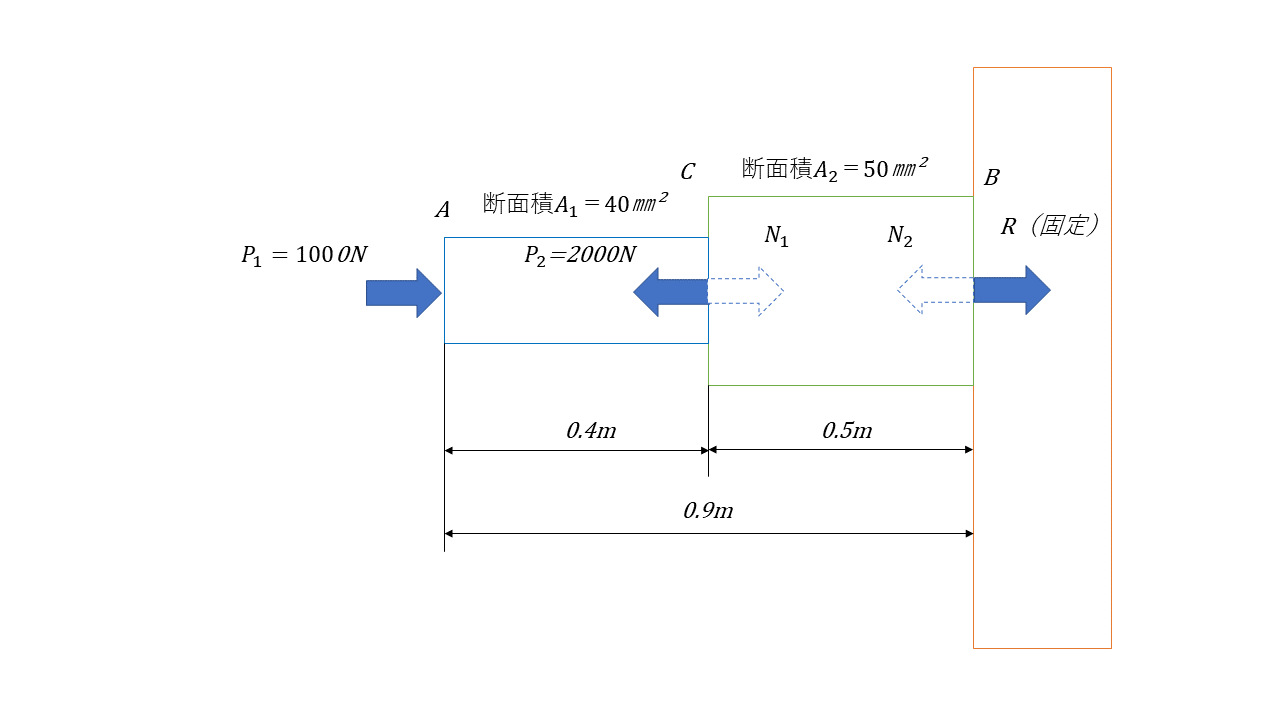
AC間の軸力
AC間の軸力に着目する。力のつり合いにより、P1とP2が同時に作用しているので、N1はP1とP2の合計で表すことができる。下記の通り、マイナスの力が働いているので、圧縮応力がかかることがわかる。

CB間の軸力
CB間の軸力に着目する。力のつり合いにより、N2と、P1とP2(つまりN1)が同時に作用しているので、この2つの合計は0になる。

R(壁)の軸力
R(壁)の応力は、CB間の引張応力と同じになるので、Rは次のようになる。

AC間の応力の計算
AC間の応力は、力/断面積で表されるので、AC間の軸力は次の通りになる。

CB間の応力の計算
同じようにCB間の応力は、次の通りになる。
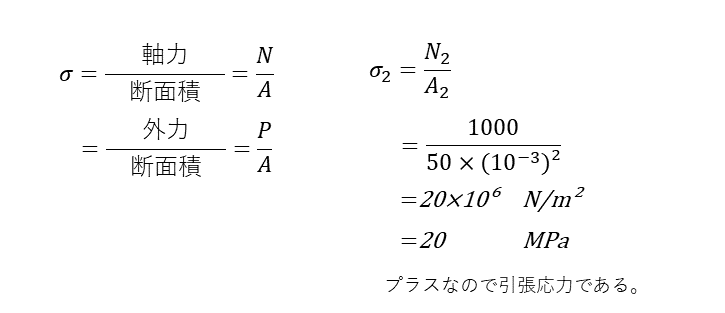
伸びの計算
材料(青)と材料(緑)のそれぞれを計算する。
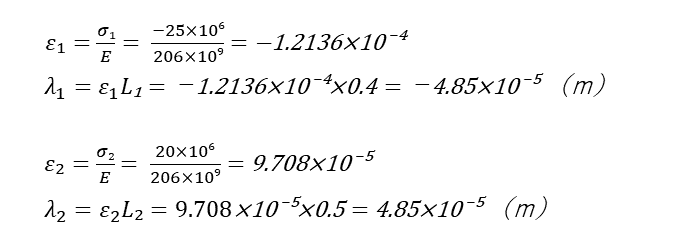
段付き全体の伸びの計算
両方を合計すれば、ACが圧縮応力によりCB間が伸びるため、段付き全体は0となる。