曲げ応力
曲げ応力とは、曲げモーメントの作用を受けて材料の内部に生じる垂直応力をいう。材料に、曲げモーメントを作用させると、上面には圧縮応力、下面に引張応力がかかり、また、伸びも縮みもかからない面を中立面、中立面とはりの断面と交わってできる軸を中立軸という。曲げ応力は「曲げモーメント×中立面」からの距離に対して、断面二次モーメントで割ることで定義づけられる。
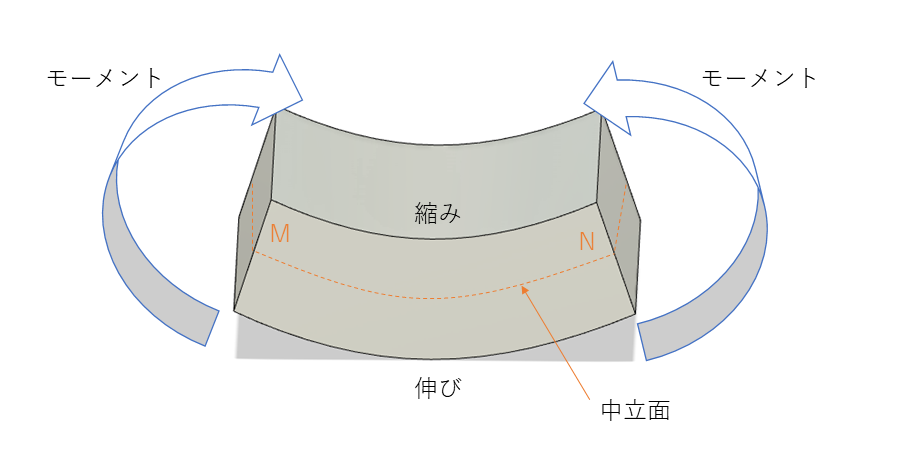
中立面
中立面とは、曲げ応力がかかる材料は上面に圧縮応力がかかり下面に引張応力がかかるが、長さがかからない面を中立面という。また、中立軸とは、材料の任意の断面と中立面の交線である。中立軸は、各任意の断面重心を通るため、曲げ応力はかからない。
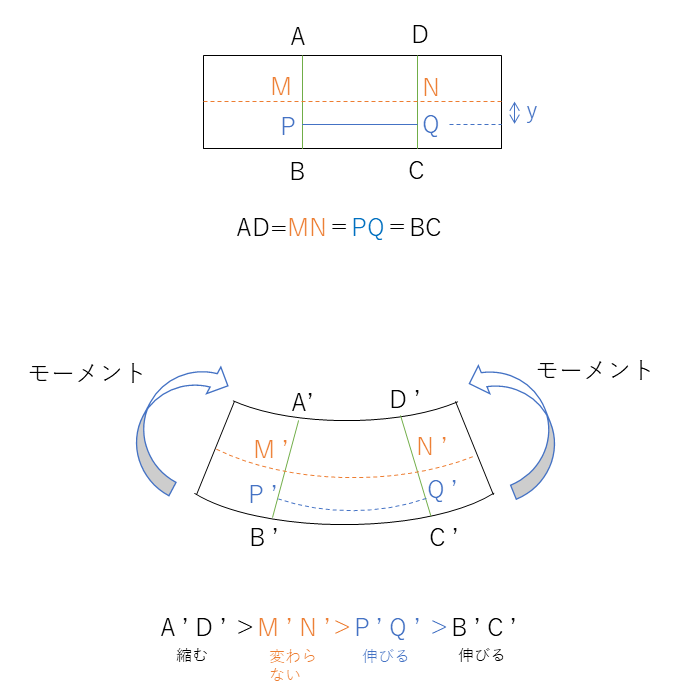
曲げモーメントの断面
曲げ応力がかかっている材料の断面をとると、次のようになる。曲げ応力の大きさは中立面から離れるに比例して大きくなる。曲げ応力が上にいくに従い圧縮応力がかかり、下にいくに従い、引張応力がかかるが、上面下面でそれぞれ応力は最大になる。
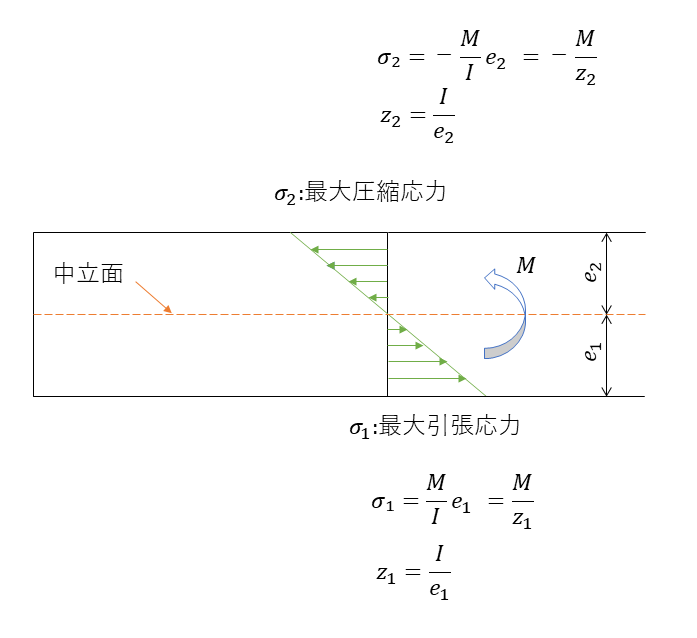
曲げ応力
曲げ応力は、次式で表される

曲げモーメント
曲げモーメントは、次式で表される
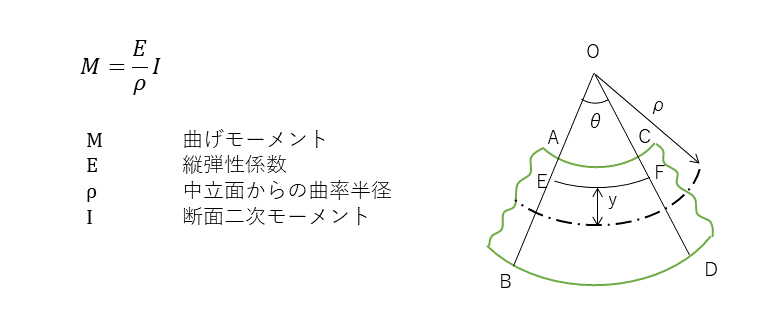
曲げ応力と曲げモーメント
曲げ応力と曲げモーメントの関係は、次式で表される。また、断面二次モーメントは、材料の断面でわかっており主なものを下記で記載している。

断面二次モーメントIと断面係数Z
断面二次モーメントは、Iで表され、材料の断面形状で異なり、断面形状の特性を表す係数である。また、断面係数とは、中立軸に関する値で、Zで表される。断面係数が大きい断面形状ほど、最大曲げ応力は小さくなり、大きな曲げモーメントも耐えることができる。一方で断面積は小さくする必要がある。
四角
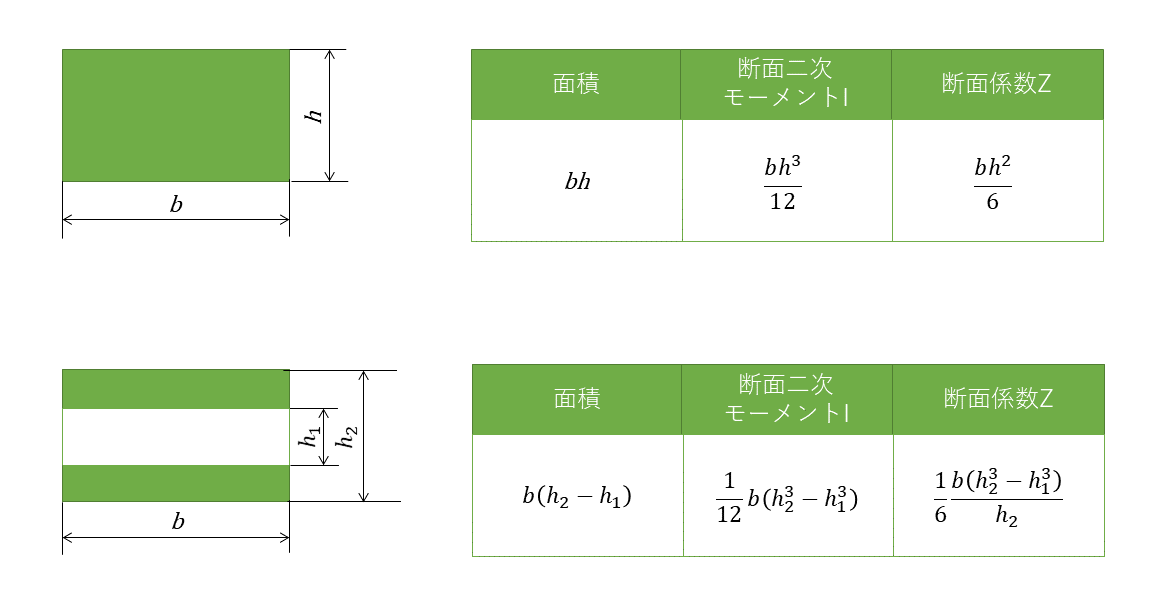
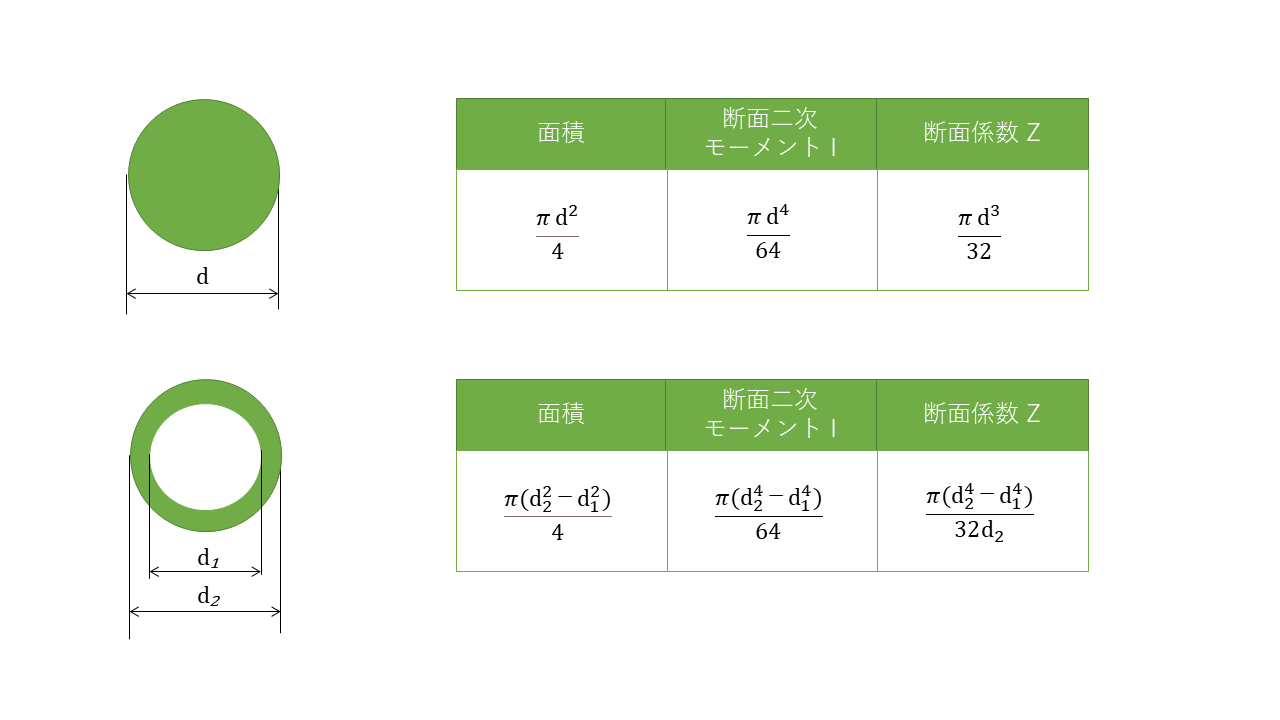
円
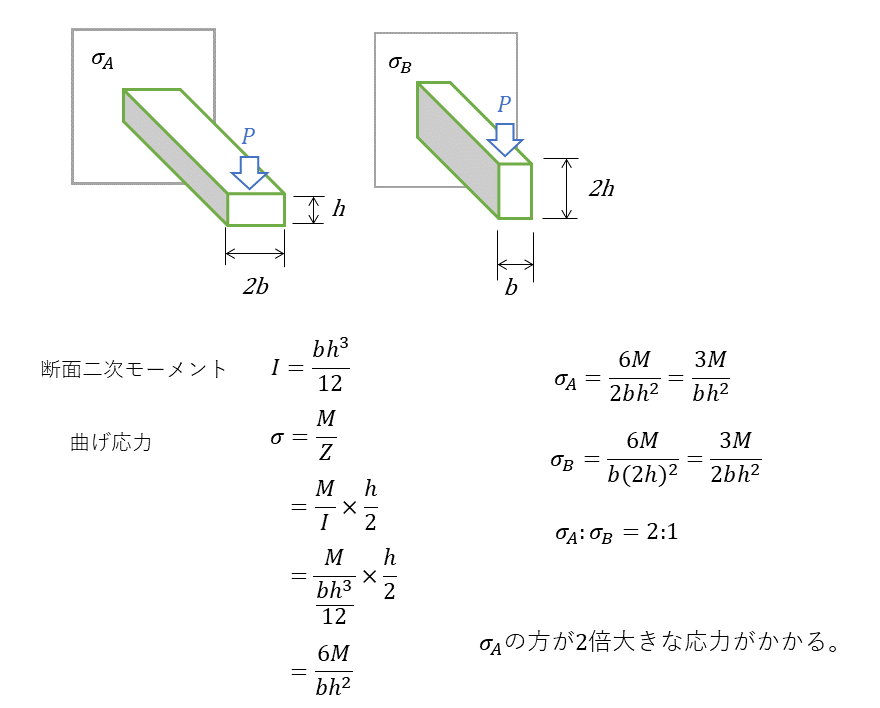
曲げ応力の比較
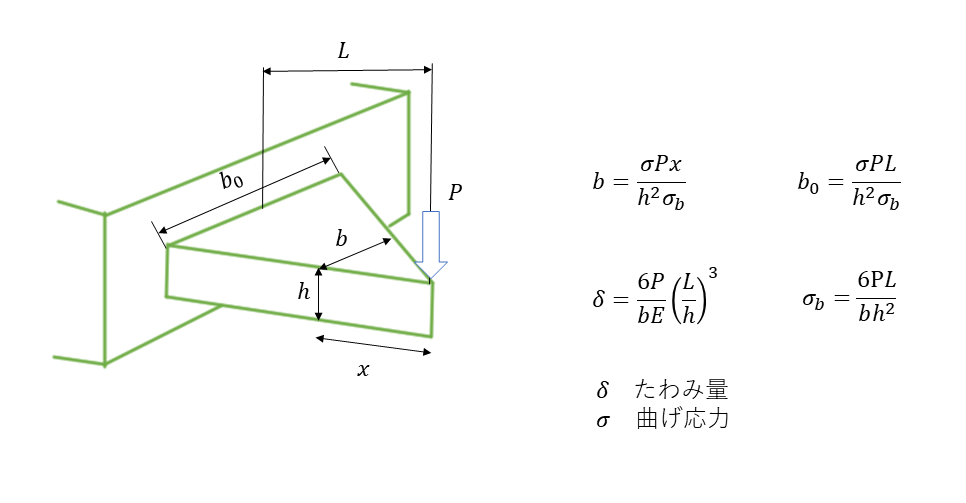
片持ちはりを例に、曲げ応力の比較を行った。下記に示した通り、縦長(h)が長いほうが、曲げ応力が小さくなることがわかる。
はりの平等強さ
危険断面に生じる曲げ応力は許容応力以下にする必要があるが、はりの断面寸法を全体にわたって同じにすると経済的なコストが高い。そのため、曲げ応力が一定値になるように曲げモーメントに比例した断面係数のはりにすれば、はり全体にわたって平等な強さになる。の発想は、三角板ばねや重ね板ばねとして活用されている。平等強さの片持ちはりを参照のこと。