応力
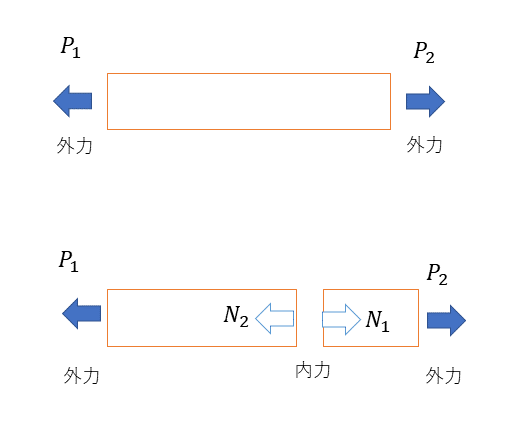
応力は、外力を受けたときの部材の材料内部に生じる内力で、内力の単位面積あたりの値と定義される。一般に引っ張られたときの引張応力、圧縮されたときの圧縮応力、ハサミで切断するようなせん断応力、曲げられた時の曲げ応力、ねじりが加わった時のねじり応力がある。応力の中でも、引張応力、圧縮応力は単純応力と呼ばれる。また、応力が生じた部分にひずみが生じるため、材料にはひずみを考慮しなければならない。
応力の単位
応力の単位には N/m2または、Pa(パスカル)を用いる。通常は大きな応力値を想定するので、1 [N/mm2] = 1 × 106[N/m2] = 1 [MPa](メガパスカル)が使われる。
垂直応力(引張応力・圧縮応力)
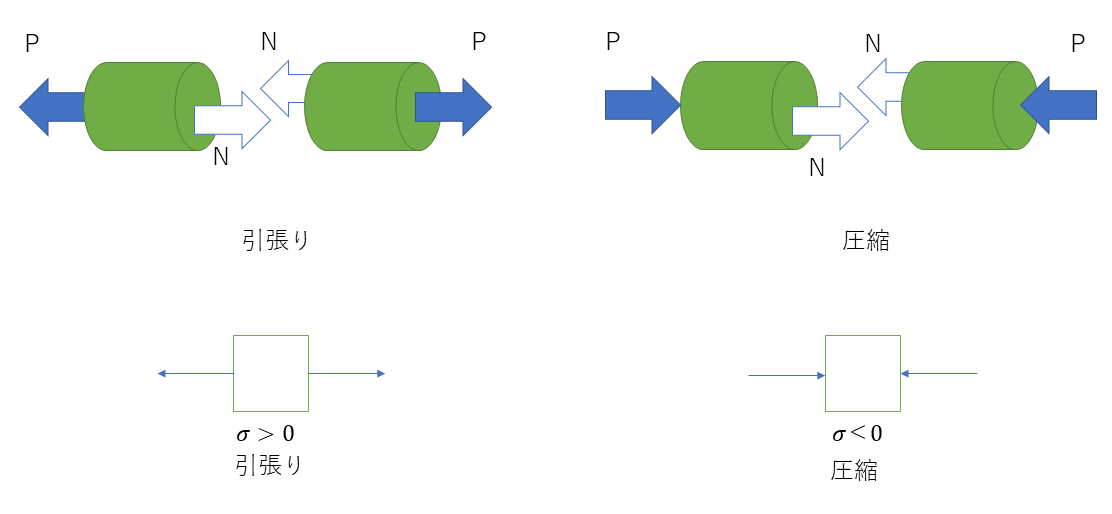
垂直応力とは引張応力、圧縮応力のことをいう。下記は、垂直応力がかかった丸棒であるが、丸棒に生じる内力(軸力)P(N)が作用する場合、丸棒の断面積をA(mm)とすると、この断面内に生ずる垂直応力σは次式で求めることができる。この時、断面積あたりどれだけの力で引っ張っているか、あるいは圧縮しているかを表したものである。
垂直応力(引張応力・圧縮応力)の式
垂直応力(引張応力・圧縮応力)は次式で表される。単位はN/m²あるいはMPaを使う。(Paは小さすぎるため。)

EXCELで計算する。
薄いオレンジのところに数字を入力すると、応力が計算できます。
せん断応力
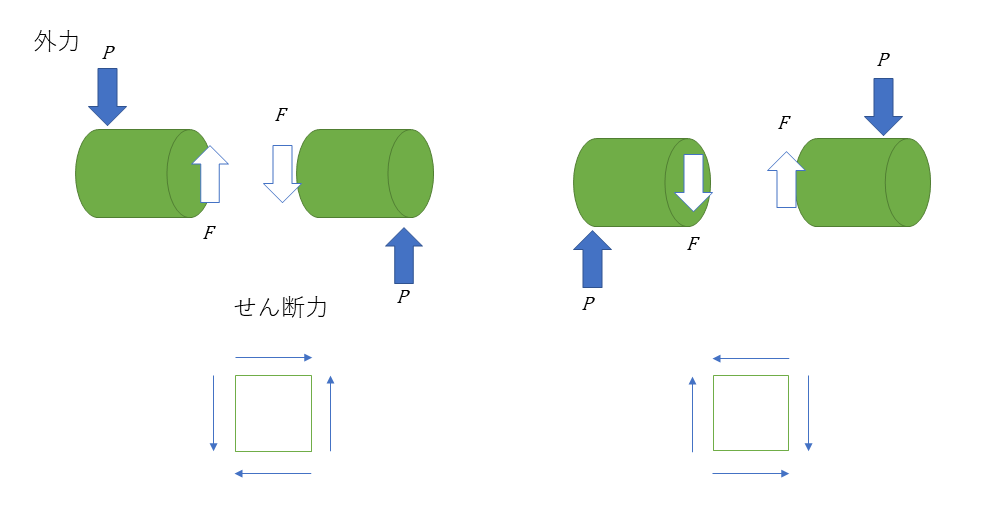
物体に断面に平行な力が働くとせん断応力が発生するが、せん断応力を断面積で割った、単位面積当たりの応力を、せん断応力という。
せん断応力の式
せん断応力の次式で表される。

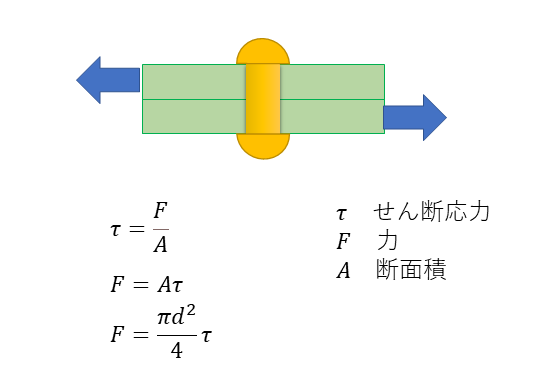
せん断応力の式例:リベットの応力
リベットに働くせん断応力は下記の通りになる。
共役せん断応力
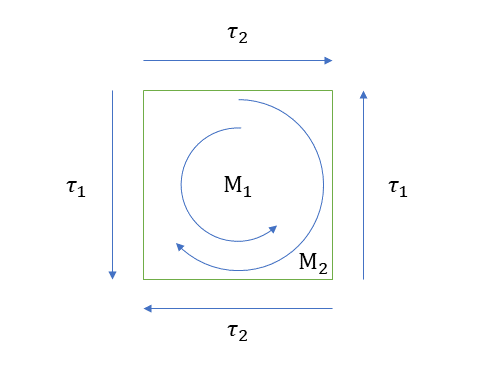
せん断力モーメントは、4つの面に作用する。反時計まわりのせん断応力M1と時計まわりのせん断応力M2が生じる。これらの応力τ1とτ2は等しいため、共役せん断応力という。
曲げ応力
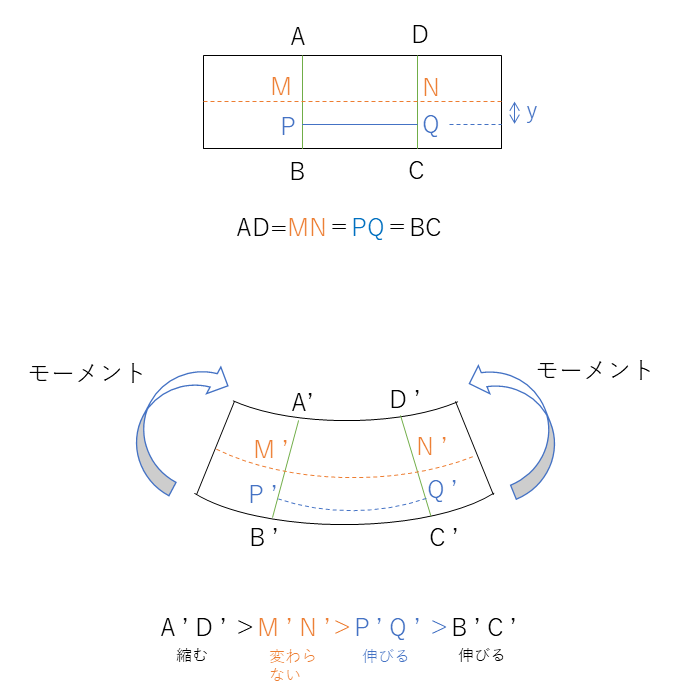
曲げ応力とは、材料の曲げの力(曲げモーメント)がかかったときの応力である。中心の中立線を基準として上方向には圧縮応力、下方向には引張応力がかかる。
曲げ応力の式
曲げ応力は、次式で表される

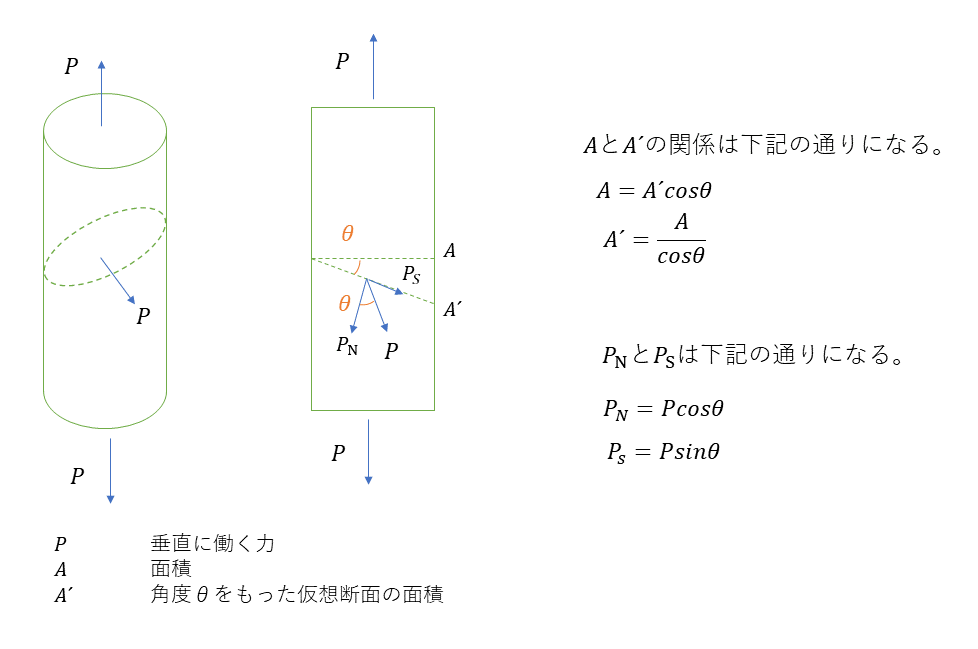
傾斜断面に発生する応力
角度θをもった斜面に対する応力は下記のように表される。
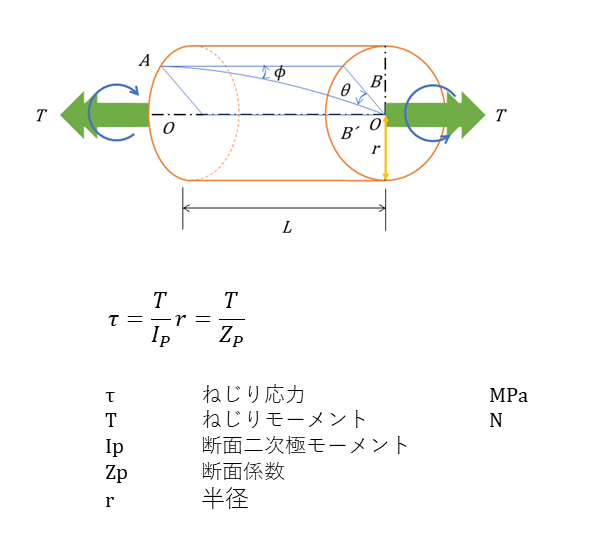
ねじり応力
ねじり応力とは、ねじりにかかる応力である。
ひずみ
ひずみとは、材料に加えられた応力により、変形することである。

応力‐ひずみ線図
弾性:材料は、力を加えると変形するが、力を取り除くと元に戻る性質がある。応力‐ひずみ線図の比例限度の部分にある。
塑性:材料は力を加えると変形し、力を取り除いても変形が残る。下降伏点以降の部分をいう。
延性破壊:よく伸びて破断することを延性破壊といい、破断に至る時間が長い材料を延性材料という。
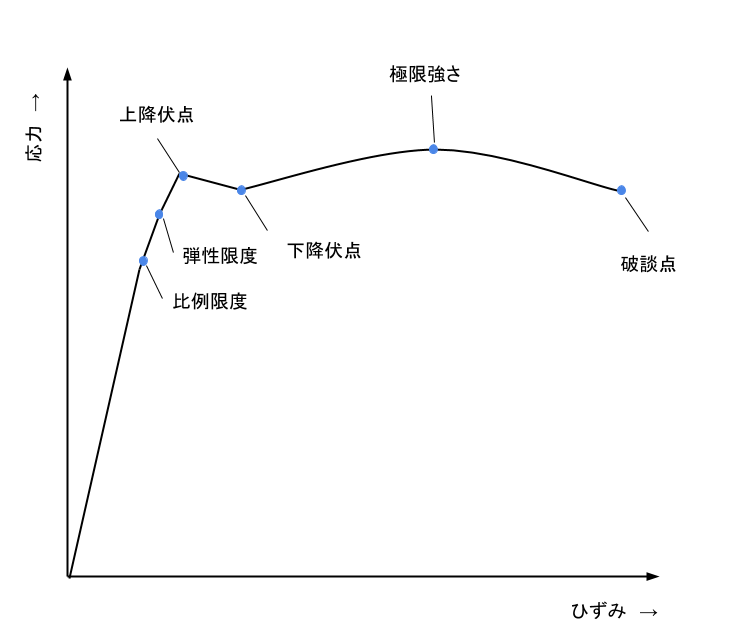
軟鋼の応力ーひずみ線図
トラス構造
クレーンや橋、建築物の設計においては、棒状の材料を結合して荷重を支える骨組構造が用いられる。結合部が、ピンでつないであれば各部材は自由に回転できるため、部材には引張力や圧縮力を受けるだけであるが、部材を溶接などで回転できないように接合すると、モーメントという回転させようとする反力を余分に生じることになる。部材の連結部を節と呼び、滑節のみからなる骨組構造をトラス構造、剛節のみからなる骨組構造をラーメン構造という。
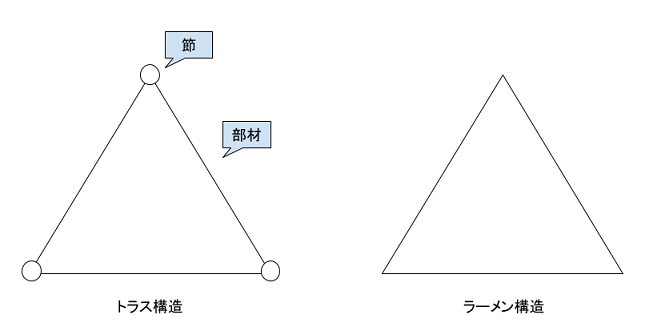
骨組構造