フックの法則
フックの法則(Hooke’s law)は材料力学の基礎的な概念で、弾性変形において応力とひずみが比例するという関係を示す式である。イギリスの物理学者ロバート・フック(1635―1703) によって、応力とそれによる変形の大きさが比例することを発見した。
フックの法則
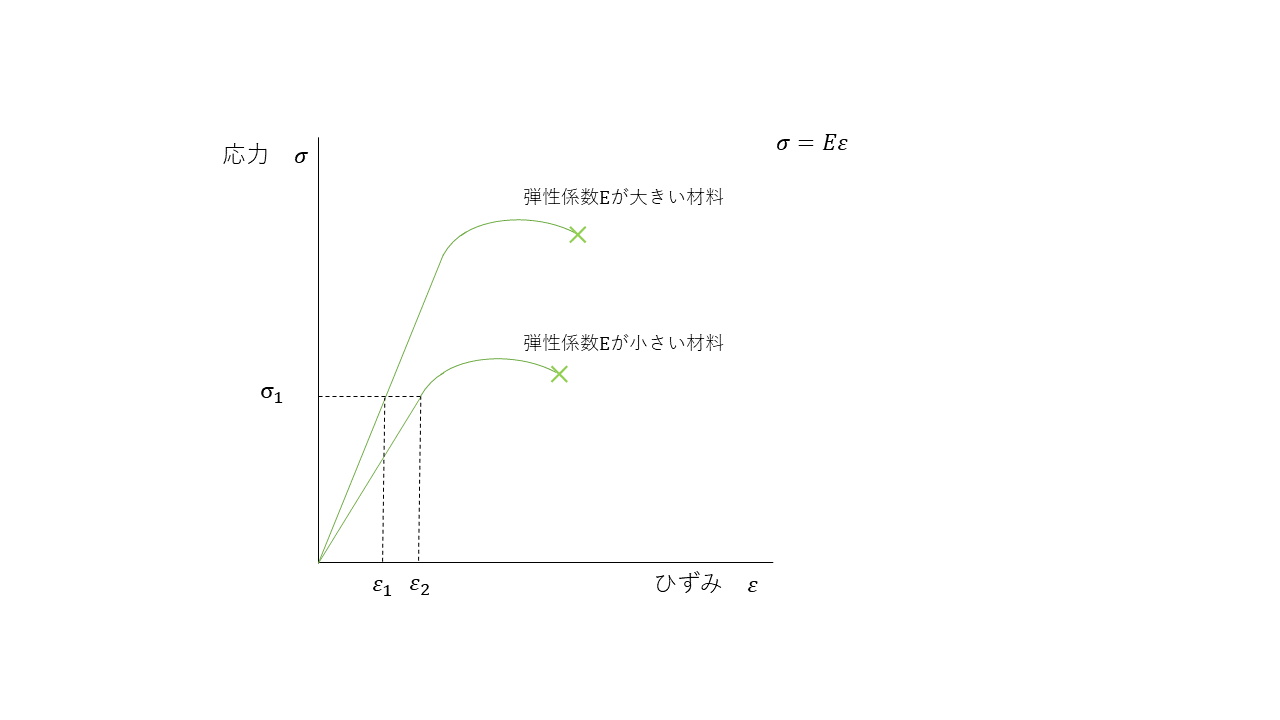
フックの法則は次式で表される。ヤング率Eは(縦弾性係数)を表し、εは縦ひずみを示す。
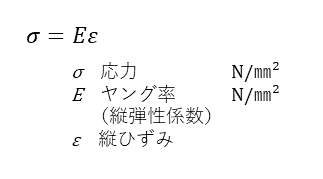
ヤング率(縦弾性係数)
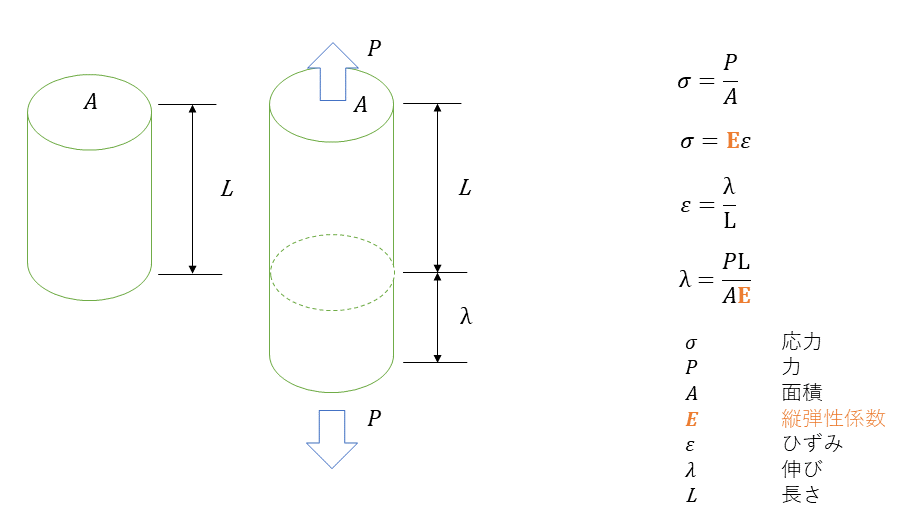
ヤング率(縦弾性係数)は垂直応力と縦ひずみとのフックの法則における比例定数である。次のグラフで表されるようにヤング率Eが大きければ大きいほど、「ひずみ難い材料」であるといえ、大きな応力にも耐えることができる。トーマス・ヤング(1773―1829)が現在のヤング率に相当する量(ヤング率と断面積との積)を測定している。単位は109[N/m2]=1[GPa]。
せん断応力とせん断ひずみ
フックの法則と同じように、せん断応力とせん断ひずみの間にも比例関係が成立する。

せん断弾性係数(横弾性係数)
Gは、せん断弾性係数(横弾性係数)といい、材料の持つ固有の値である。
ポアソン比
ポアソン比(Poisson’s ratio)とは、縦ひずみと横ひずみ比である。また、その逆数をポアソン数 (Poisson’s number)という。ポアソン比は材料固有の値であるが、たいていの金属材料では1/4から1/3の間で収まり、比例限度内では、一定の値になる。
縦弾性係数・せん断弾性係数・ポアソン比
縦弾性係数・せん断弾性係数・ポアソン比の間には次式の関係がある。

主な材料の縦弾性係数・せん断弾性係数・ポアソン比
| 材料 | E[Gpa] | G[Gpa] | ポアソン比ν |
|---|---|---|---|
| 軟鋼 | 206 | 82 | 0.28-0.3 |
| 硬鋼 | 200 | 78 | 0.28 |
| 鋳鉄 | 157 | 61 | 0.26 |
| 銅 | 123 | 46 | 0.34 |
| 黄銅 | 100 | 37 | 0.35 |
| チタン | 103 | – | – |
| アルミニウム | 73 | 26 | 0.34 |
| ジュラルミン | 72 | 27 | 0.34 |
| ガラス | 71 | 29 | 0.35 |
| コンクリート | 20 | – | 0.2 |