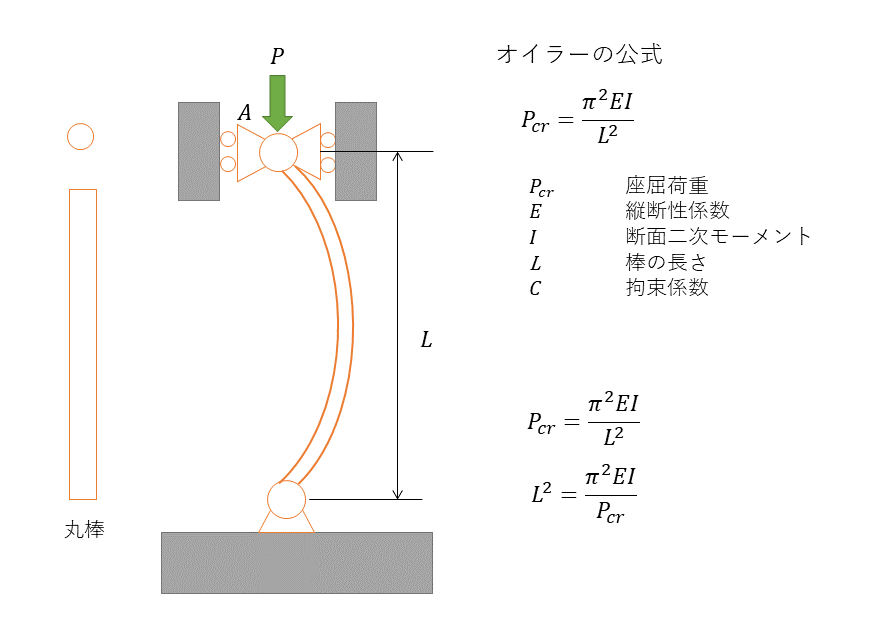
オイラーの公式
オイラーの公式とは材料力学の式で座屈を表す式である。座屈に関する式は、その他、テトマイヤ―の式、ジョンソンの式などがあるが、オイラーの公式では、細長い柱に適応される。オイラーの公式を用いることで、どのぐらいの荷重がかかれば柱が座屈(湾曲)するのかがわかる。
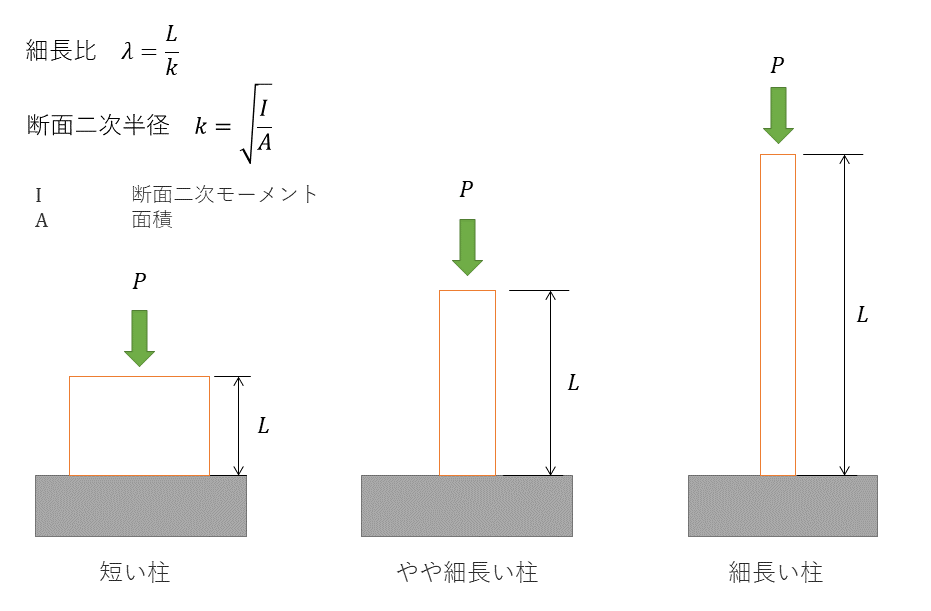
座屈
座屈とは、柱に荷重(これを座屈荷重という。)がかかった時、柱が湾曲する現象である。イメージとしては、ものさし定規に垂直方向に力がかかって湾曲する。
断面二次半径
断面二次モーメントIをAで割った値である。単位はmもしくは㎜である。
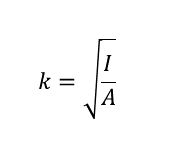
細長比
細長比とは、柱の長さLと断面二次半径kとの比で表される。オイラーの公式が適用するときは、材質による適用範囲に基づかなければならない。
オイラーの公式の通用範囲
オイラーの公式は、材料によって適用範囲が異なる。目安になる細長比は下記の通りである。
| 材質 | 鋳鉄 | 軟鋼・硬鋼 | 木材 |
|---|---|---|---|
| L/k | 80以上 | 90以上 | 100以上 |
拘束係数
柱の拘束の条件によって座屈の起こりやすさやが異なる。この条件を拘束係数Cとし、それぞれ下記の通りで決まっている。

オイラーの公式の座屈荷重

オイラーの公式に基づく座屈応力

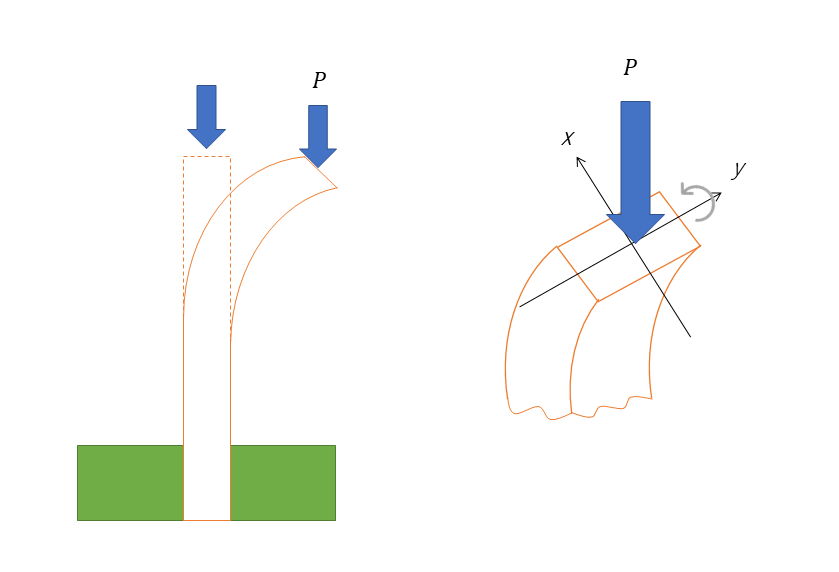
オイラーの公式の例
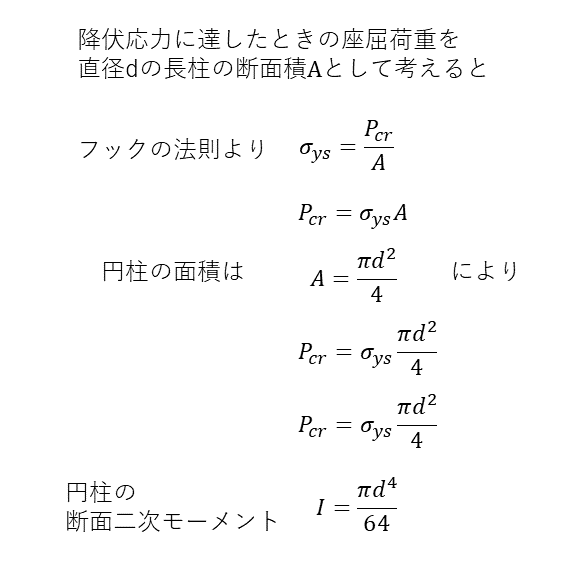
下記のような円柱の棒の座屈を考える。両端を回転事由に指示して、Aから圧縮荷重がかかっている。このとき、座屈荷重Pcrにオイラーの公式を適用できるものとする。このとき、降伏応力に達するまで座屈にいたらないようにするためにはどのくらいの棒の長さにすればいいのか、を考える。
条件の整理
この際の条件を整理すると下記のようになる。
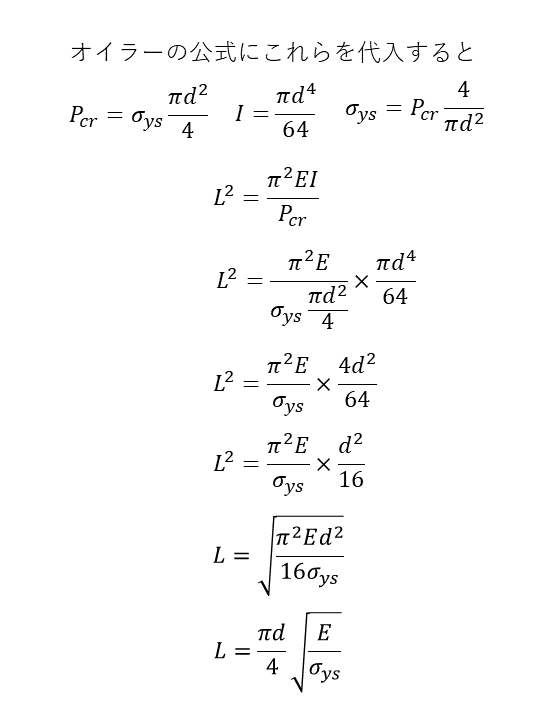
オイラーの公式に代入する
これらをオイラーの公式に代入し、長さLで整理すると、下記のような値になる。長さLはこの式で表される長さ以下にしなければならない。