運動量方程式
運動量方定式とは、ニュートンの運動の第二法則により、運動量の単位時間あたりの変化は物体に作用する外力に等しくなるという関係式である。運動方程式ともいわれる。
Table Of Contents
ニュートンの運動量方程式
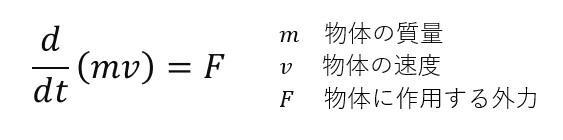
運動量方程式
流体の運動量方程式
運動量方程式を流体に適用するこのような式になる。
流体の運動方程式
流体（噴流）が壁に与える力
噴流が壁にあたる場合を考慮すると、下記のように表すことができる。
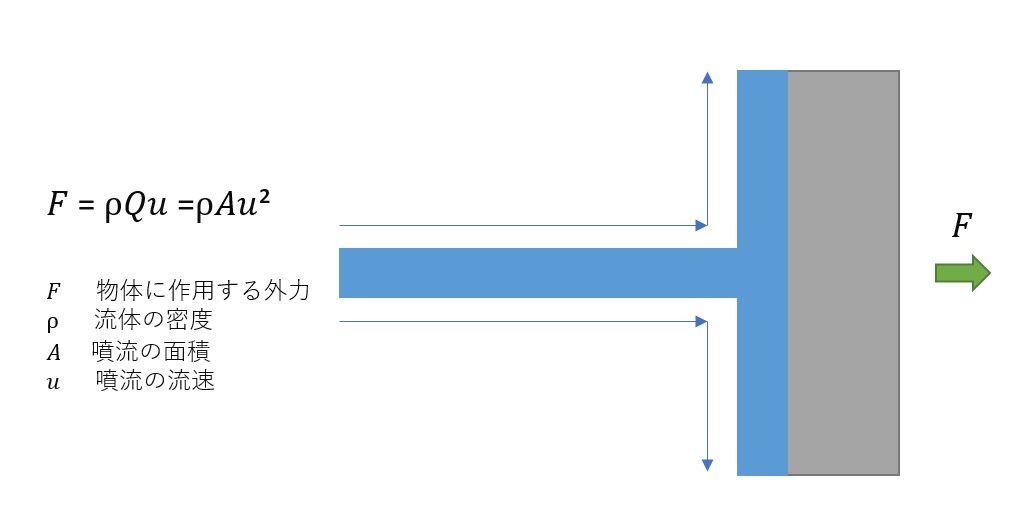
噴流から受ける力
流体が配管に与える力
配管の曲がり部(角度90°)を考えるとき、下記の通り、x方向の運動量がρQuから0になり、y方向の運動量は0からρQuになる。2方向の合力は√2ρQuとなる。
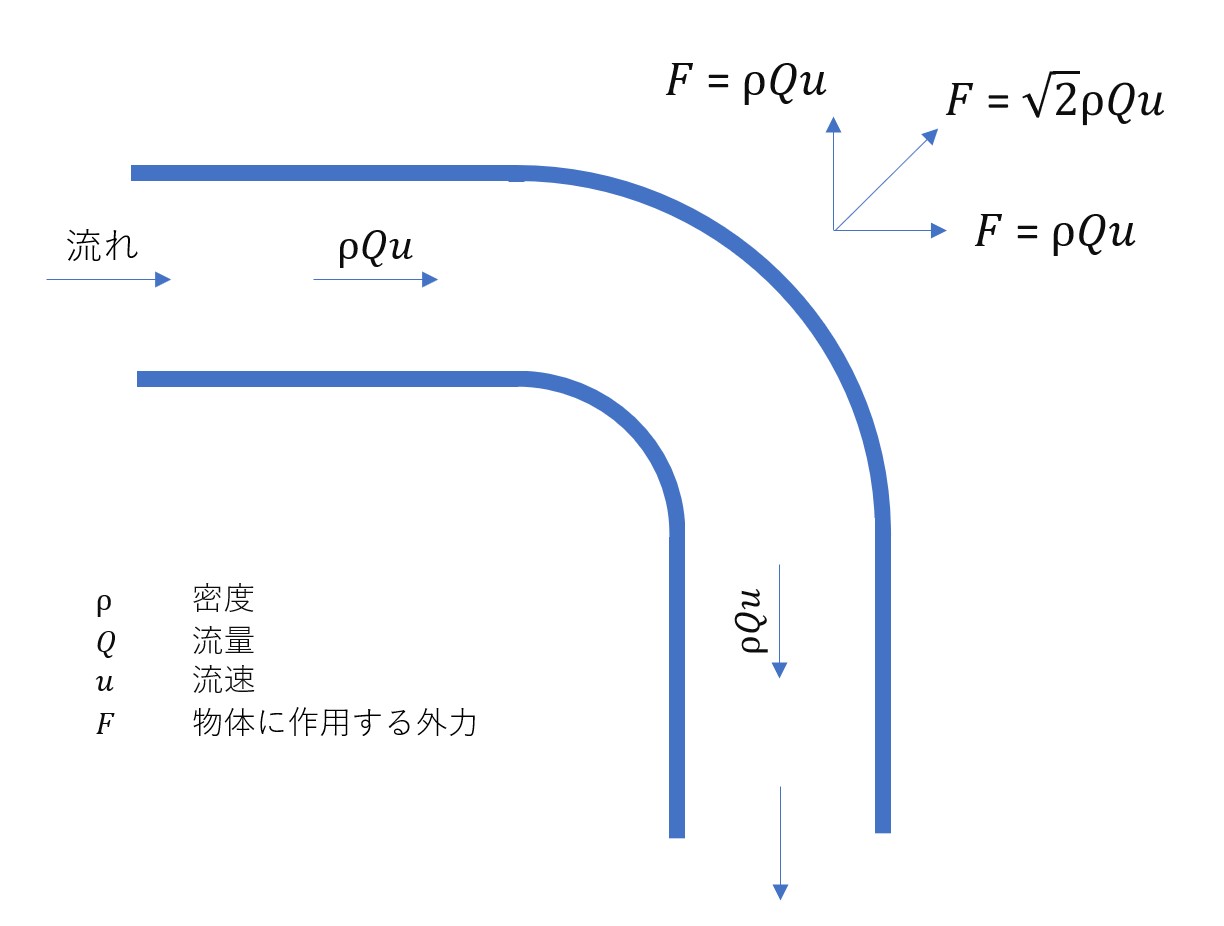
配管に加わる力