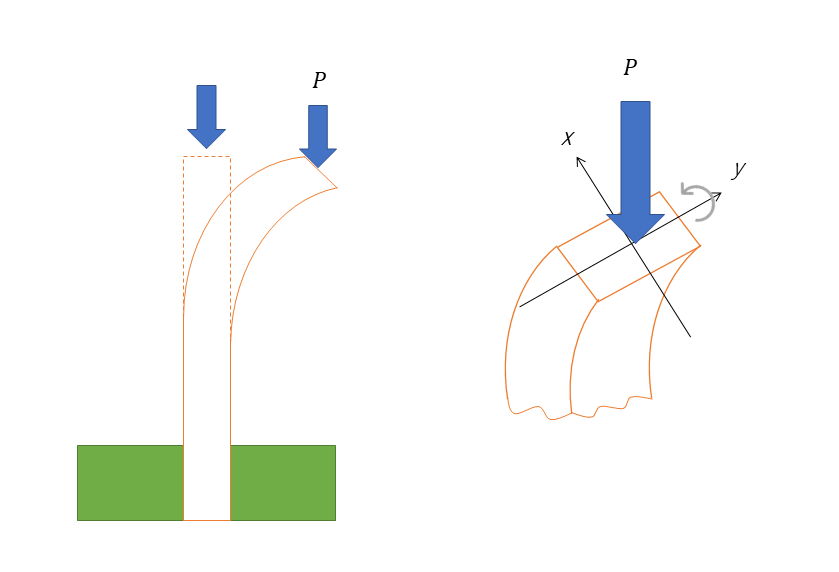
座屈
座屈（buckling）とは、構造物の柱（column）に対して、軸方向に圧縮荷重が加わると、部材が大きく湾曲する現象である。柱に想定以上の荷重を受けると、まず座屈し、いずれ破壊にいたる。座屈の計算方法として、オイラーの式やランキンの式などがあるが、どれを採用するかは細長比（短い柱、やや細長い柱、細長い柱）で決まる。
Table Of Contents
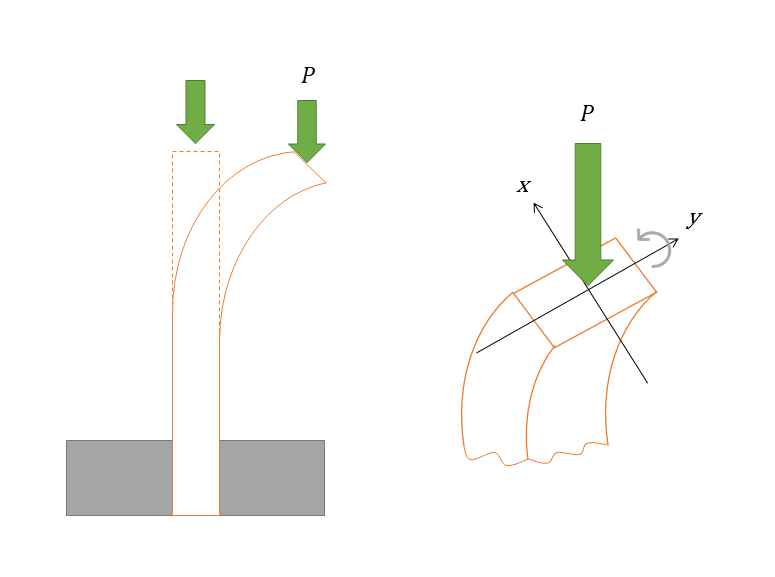
座屈荷重
座屈荷重とは、座屈を起こす最小の荷重である。
座屈応力
座屈応力は、座屈荷重と断面積の積をとり、断面積で割った値である。座屈応力が座屈荷重以下に設定する必要がある。
断面二次半径
断面二次モーメントIをAで割った値である。単位はmもしくは㎜である。
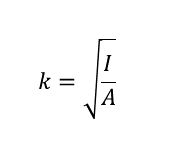
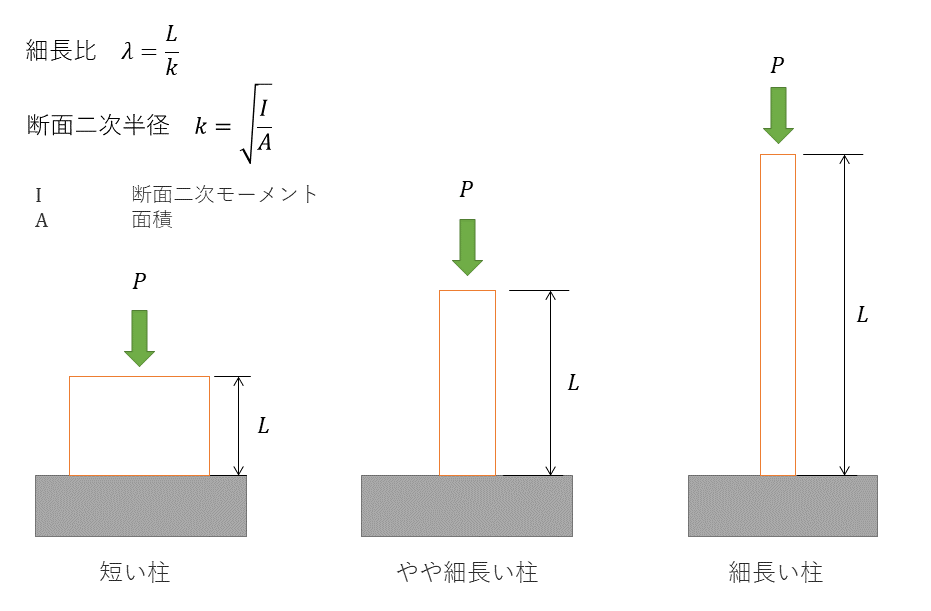
細長比
柱の長さLと断面二次半径kとの比λを細長比という。細長比によって、短い柱、やや細長い柱、細長い柱の3種類に分類できる。
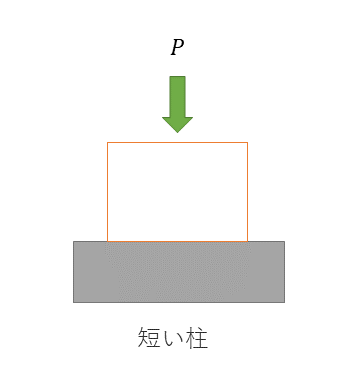
短い柱の場合(圧縮応力)
短い柱は圧縮応力を分析するだけで座屈を解析できる。
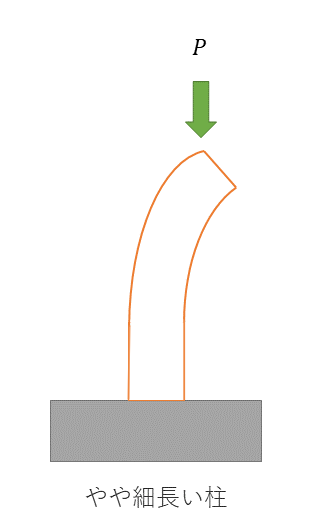
やや細長い柱の場合(ランキンの式、テトマイヤ―の式、ジョンソンの式)
やや細長い柱には、ランキンの式、テトマイヤ―の式、ジョンソンの式などで座屈を解析することができる。
ランキンの式
ランキンの式は次式の通りになる。
テトマイヤ―の式
テトマイヤーの式はaの単位はMPaで、b,cは実験により下記の通りに決まっている。
ジョンソンの式
ジョンソンの式は下記の通りになる。
細長い柱の場合(オイラーの式)
細長い柱には、オイラーの式で座屈を解析することができる。
拘束係数
細長い柱は、柱の拘束の条件によって座屈の起こりやすさやが異なる。この条件を拘束係数Cとし、それぞれ下記の通りで決まっている。
オイラーの座屈理論
オイラーの座屈理論により、細長い柱の座屈荷重Pcrは下記で求められる。
オイラーの座屈理論に基づく座屈応力
