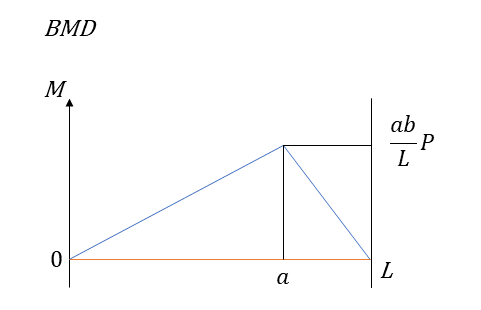単純支持はり simply support beam
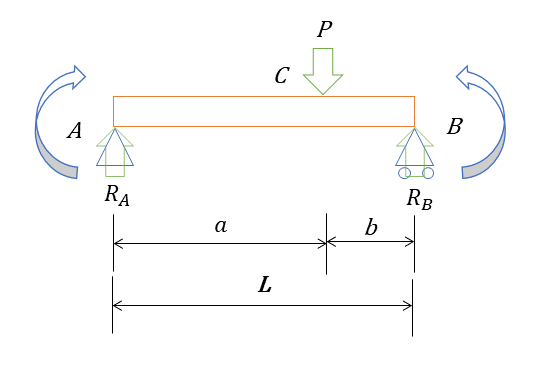
単純支持はりにおいて、はりに加わる荷重を支点または固定端で支え、はりがつり合っている状態を単純支持はりという。両端で支持されていることから両端支持はりともいう。
単純支持はりの力とモーメントのつりあい
単純支持はりでは、力(PとRA,RB)のつりあいと、点A、点Bのモーメントのつりあいに着目することで、それぞれを理解できる。
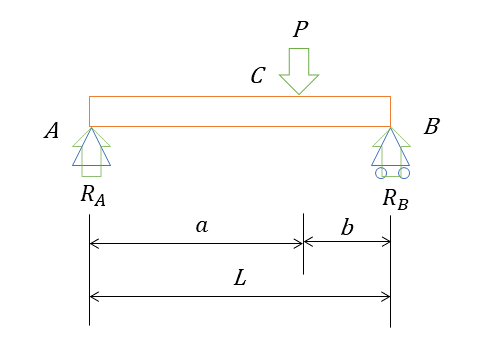
力のつりあい
PとRA,RBとは、つりあっているので下記の次式で表される。
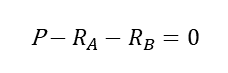
モーメントのつりあい
点Aに着目したとき、モーメントは距離×荷重で表されるため、時計回りのモーメントはaPで表され、反時計回りのモーメントはLRAで表される。正負は反時計回りを+、反時計回りを-で表すことが多いが、反していれば逆でも可。
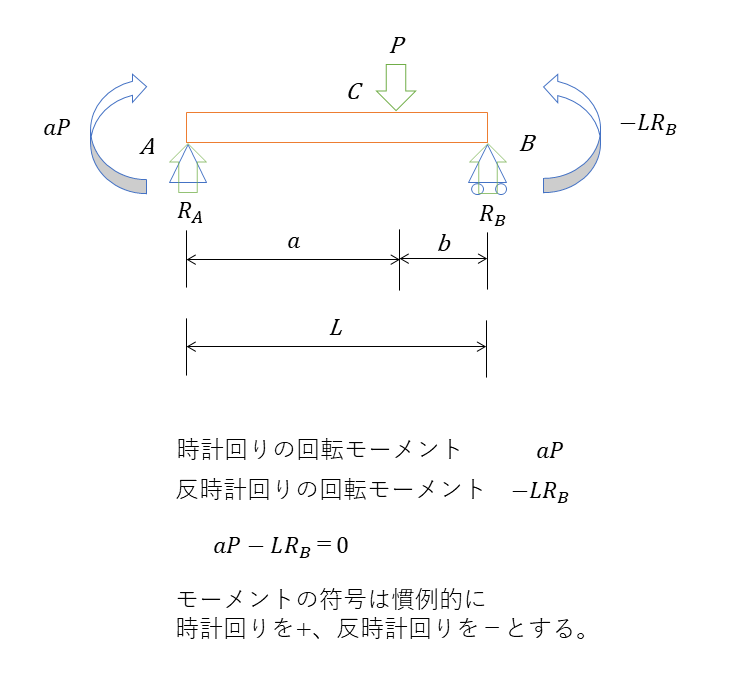
力とモーメントのつりあいから
力とモーメントのつりあいからRA,RBを導くことができる。
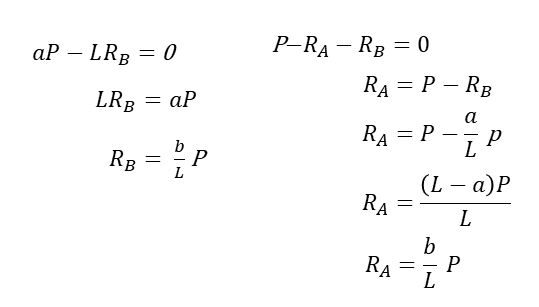
単純支持はりのせん断力
単純支持はりに力やモーメントがかかると、はりには、せん断力(内力)がかかる。RAに着目し、(0≦𝑥≦𝑎),(𝑎≦𝑥≦L)に分けて考える必要がある。
0≦𝑥≦𝑎
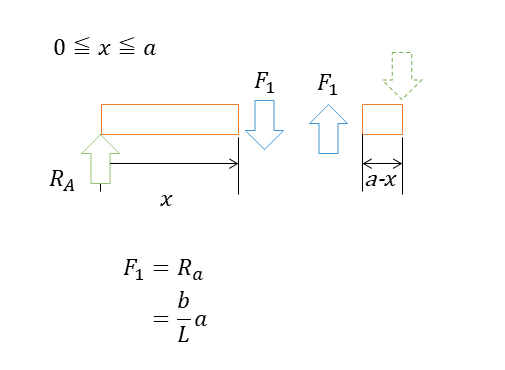
0≦𝑥≦𝑎の間のせん断力F1は下記の図のように働いている。F1とRaは等しい。
𝑎≦𝑥≦L
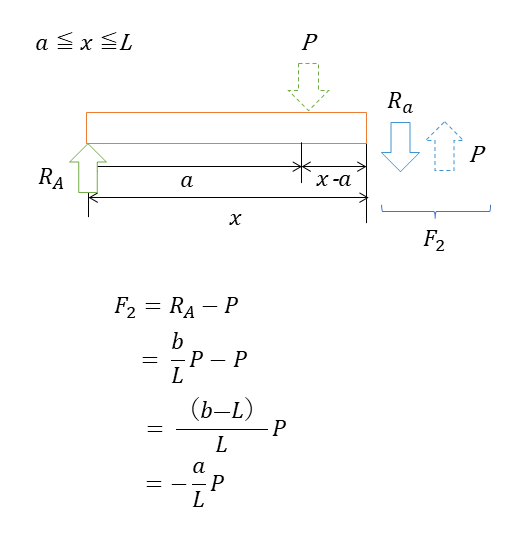
𝑎≦𝑥≦Lの間のせん断力F2は下記の図のように働いている。この区間では、Pの影響を受けるため、F2は、RaからPを引いたものが等しくなる。
単純支持はりの曲げモーメント
単純支持はりに力やモーメントがかかると、はりには、曲げモーメント(内力)がかかる。曲げモーメントは、はりの上面が凹となる場合を正、凸となる場合を負として定義される。曲げモーメントは、モーメント荷重ではなく内力としてとらえることができる。
0≦𝑥≦𝑎
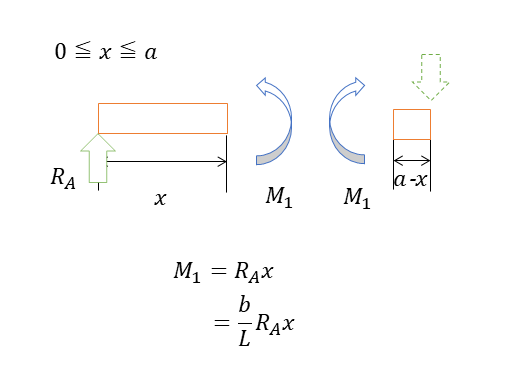
0≦𝑥≦𝑎の間の単純支持はりの曲げモーメントM1は下記の図のように働いている。なお、曲げモーメントは、距離×荷重で表される。
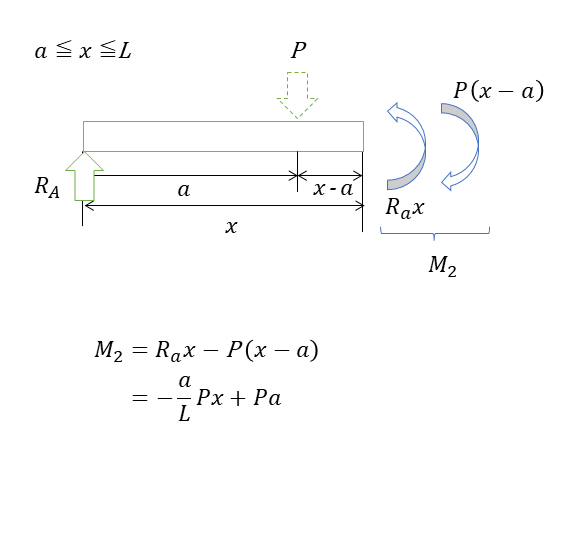
𝑎≦𝑥≦L
𝑎≦𝑥≦Lの間の曲げモーメントM2は、Pが及ぼす曲げ―モーメントを引く形で下記の図のように働いている。
せん断力図(SFD)と曲げモーメント図(BMD)
せん断力を表した図示したものをせん断力図(SFD)と曲げモーメントを図示したものを曲げモーメント図(BMD)という。それぞれはりを横軸として表現されている。
せん断力図(SFD)
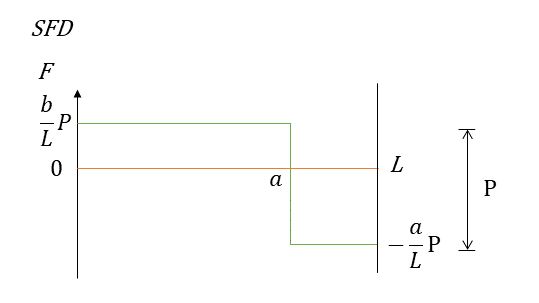
曲げモーメント図(BMD)